A métrica de Kaboudan: explorando a previsibilidade de séries temporais
Avaliando a importância da ordem temporal em modelos preditivos
A previsibilidade de uma série temporal é um aspecto essencial na modelagem preditiva, pois ajuda a determinar a viabilidade de previsões confiáveis e guiar a escolha de modelos. Para medir essa previsibilidade, uma abordagem possível é a métrica de Kaboudan, que avalia como a ordem dos dados em uma série influencia o desempenho preditivo de modelos.
Entendendo a métrica de Kaboudan
Proposta em 1999, a métrica de Kaboudan se baseia em comparar o desempenho preditivo de um modelo aplicado à série original com seu desempenho em uma versão embaralhada da mesma série. Esse embaralhamento é realizado em blocos de dados. A fórmula utilizada é:
Onde:
SSE_Y: Soma dos erros quadráticos de previsão para a série original.
SSE_S: Soma dos erros quadráticos de previsão para a série embaralhada.
Se a ordem dos dados importa para a previsão, SSE_Y será significativamente menor que SSE_S, resultando em uma métrica próxima de 1. Caso contrário, e SSE_Y e SSE_S serão similares, com métrica próxima de 0.
Dados e modelos utilizados
Para avaliar a previsibilidade, analisamos duas séries temporais distintas:
Crescimento mensal do PIB (à taxa m/m): Representa a variação percentual do Produto Interno Bruto entre meses consecutivos. É esperado que a série apresente padrões sazonais e de longo prazo relacionados a ciclos econômicos.
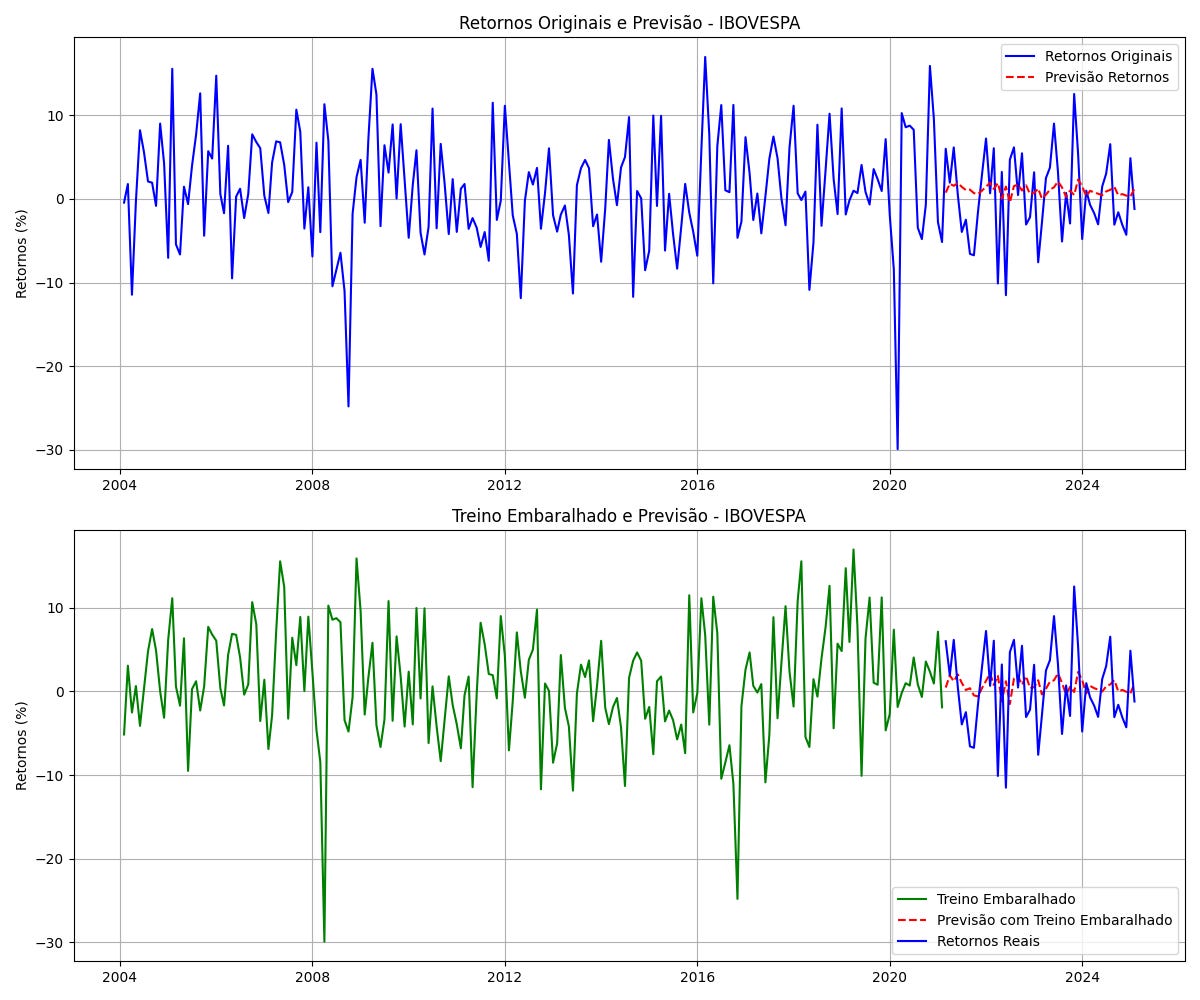
Retornos mensais do IBOVESPA: Corresponde à variação percentual do índice da bolsa brasileira. Como é uma série financeira, há maior imprevisibilidade devido à alta volatilidade e ao comportamento especulativo do mercado.
Modelos diferentes foram utilizados para cada série:
SARIMA para o PIB: Este modelo é ideal para capturar padrões sazonais e tendências estruturais, comuns em dados econômicos.
GARCH para o IBOVESPA: Séries financeiras frequentemente apresentam heterocedasticidade, o que torna o modelo GARCH mais adequado para modelar a variância condicional dos retornos.
Metodologia
Os dados foram separados em conjuntos de treino e teste, com o teste compreendendo os 48 meses mais recentes. Para cada série, foram calculados os erros quadráticos de previsão (SSE_Y) e também os erros após embaralhar blocos de 12 meses (SSE_S). O embaralhamento em blocos garante que a sazonalidade "intra-bloco" seja preservada, mas destrói relações temporais de longo prazo. Caso deseje reproduzir os resultados, o repositório pq_kaboudan possui todo o código utilizado.
Resultados
Os resultados da análise de previsibilidade para o período 2004-2024 foram os seguintes:
PIB:
SSE Original: 0.025962
SSE Embaralhado: 0.140960
Métrica de Kaboudan: 0.815818
IBOVESPA:
SSE Original : 0.125431
SSE Embaralhado: 0.124806
Métrica de Kaboudan: 0.00000
Esses valores ilustram dois comportamentos distintos. Para o PIB, após o embaralhamento, ocorreu um aumento significativo do erro de previsão, o que indica que a estrutura da série original forneceu informações significativas para o modelo. Isso mostra que a ordem dos dados é crucial para sua previsão e também diz respeito a previsibilidade da série, indicando que a previsão aproveitou a ordem temporal existente e que as variações ao longo do tempo não são puro ruído e dão, de fato, informação. Em contraste, para o IBOVESPA, a pequena diferença entre os erros revela que a com pouco ganho informacional na organização temporal dos dados.
Discussão
A métrica de Kaboudan se mostra útil para avaliar o impacto da estrutura temporal em diferentes contextos. No entanto, ela possui limitações importantes:
Dependência do modelo preditivo: Resultados podem variar conforme a escolha e o ajuste do modelo.
Sensibilidade ao tamanho dos blocos: O embaralhamento pode ser influenciado pela escolha de blocos maiores ou menores.
Interpretação em séries imprevisíveis: Em contextos como mercados financeiros, a métrica reflete mais a natureza aleatória da série do que falhas no modelo.
A aplicação dessa métrica é particularmente valiosa para compreender padrões temporais em séries econômicas e financeiras. Contudo, deve ser usada em conjunto com outras análises para uma avaliação mais completa da previsibilidade das séries temporais.
Até a próxima!