Cálculo atuarial de pensões por morte (função heritor) em planos BD
Como calcular, em anos de benefício, o encargo e a reserva de pensão por morte em planos BD usando PNAD Contínua 2023, credibilidade e tábua AT-2012.
Introdução
As pensões por morte representam um benefício vitalício ou temporário pago aos dependentes de um participante falecido em planos previdenciários de Benefício Definido (BD). Calcular de forma precisa o custo atuarial desses benefícios é fundamental para fundos de pensão (EFPC) e seguradoras, pois afeta a solvência e o pricing de produtos de risco.
A avaliação de encargos e reservas de pensão por morte auxilia na gestão de riscos biométricos: por exemplo, quantificar quantos anos de benefício, em média, custará a pensão dos dependentes de um participante que venha a falecer em determinada idade.
Este artigo explora a metodologia implementada no projeto pq_heritor, que calcula de forma granular o encargo atuarial e a reserva matemática associados à pensão por morte, com base em dados demográficos brasileiros.
Serão abordadas as fontes de dados utilizadas (PNAD Contínua), as metodologias desenvolvidas em cada etapa (tábua de conjugalidade, distribuição de diferença etária – age gap –, distribuição de filhos dependentes) e as premissas atuariais adotadas para o cálculo do encargo (benefício por morte) e da reserva técnica correspondente.
Convém destacar que tais cálculos são úteis em situações como: projeção do passivo atuarial de planos BD com pensão por morte, definição de prêmios de seguro ou contribuições necessárias para cobrir o risco de morte de participantes, e análise de sensibilidade a mudanças demográficas (por exemplo, tendências de menores taxas de casamentos ou fecundidade) no contexto previdenciário.
Função de heritor é a função que, dada a idade/sexo do participante e a composição familiar estimada (conjugalidade, age gap e filhos), retorna o valor presente esperado das pensões por morte em “anos de benefício”, base para o cálculo de encargo e reserva em planos BD/EFPC.
Em suma, a função de heritor desenvolvida visa aprimorar as bases técnicas para avaliação de pensão por morte, fornecendo subsídios a analistas quantitativos e atuários na tomada de decisões informadas em EFPC e regimes previdenciários BD.
O presente trabalho é somente um exercício para servir de referência. A realidade de cada fundo de pensão é um caso particular, a ser analisado com cuidado.
Fonte de dados e população alvo
A base de informações demográficas utilizada é a Pesquisa Nacional por Amostra de Domicílios (PNAD), conduzida pelo IBGE. Especificamente, foi empregada a PNAD Contínua anual, tomando os microdados de 2023 como referência para a composição familiar da população brasileira.
Este rico conjunto de dados amostrais inclui características de todos os membros do domicílio, permitindo identificar relações de parentesco, condição conjugal, número de filhos, etc. A fim de derivar hipóteses atuariais realistas, o projeto analisa tanto a população geral do Brasil quanto o subgrupo de servidores públicos estatutários.
Os servidores públicos civis são foco de interesse por possuírem perfis demográficos um pouco distintos da média da população. Por exemplo, podem apresentar taxas de casamento diferentes ou padrões familiares específicos. No entanto, como a amostra de servidores dentro da PNAD é relativamente menor, as estimativas diretas para esse grupo podem ser voláteis.
Por isso, emprega-se um modelo de credibilidade para combinar informações da população geral com as dos servidores, garantindo estimativas robustas e sem vieses. Todos os cálculos utilizam os pesos amostrais do IBGE para assegurar representatividade populacional.
Em síntese, a fonte de dados confere base empírica às hipóteses atuariais de proporção de participantes casados, distribuição de idades de cônjuges e existência de filhos dependentes, fundamentais para o cálculo do encargo de pensão por morte.
Tábua de conjugalidade (probabilidade de cônjuge por idade)
A primeira etapa da modelagem consiste em construir uma tábua de conjugalidade, isto é, estimar a probabilidade P₍c₎(x) de um indivíduo de idade x ter cônjuge (esposo/a ou companheiro/a) vivo. A PNAD fornece diretamente a condição no domicílio: considera-se que um participante possui cônjuge se no domicílio houver alguém classificado como cônjuge/companheiro(a). Os códigos 02 ou 03 na variável de relação domiciliar, que abrangem cônjuges de sexo diferente ou do mesmo sexo.
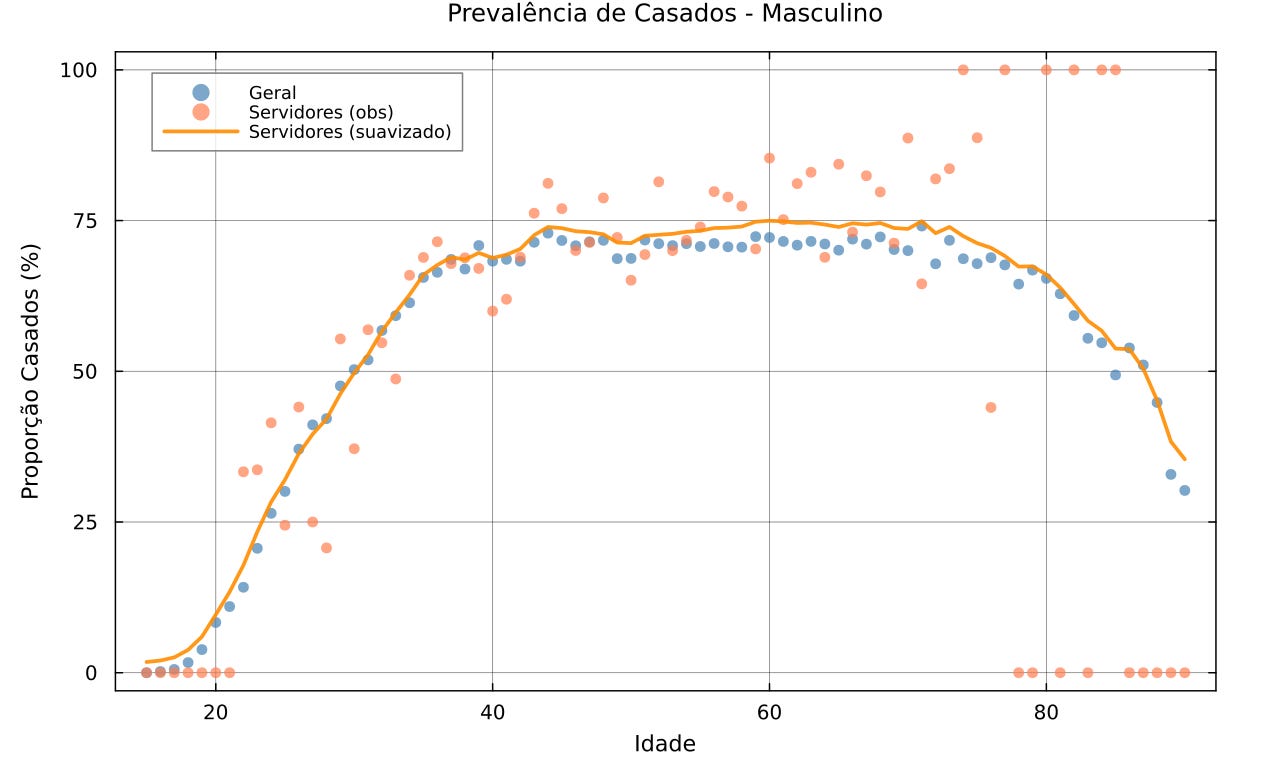
Calcula-se então, para cada idade e sexo, a proporção de pessoas casadas ou em união estável. Essa proporção varia conforme a idade: em idades jovens é baixa, devido ao grande número de solteiros, atinge um pico na meia-idade quando a maioria das pessoas já casou, e tende a cair em idades muito avançadas, especialmente para mulheres, devido à viuvez.
No projeto, obteve-se, por exemplo, que na população geral masculina a prevalência de casados atinge cerca de 80-85% por volta dos 50 anos de idade, enquanto para mulheres atinge um pico um pouco menor e declina mais acentuadamente após os 70 anos, devido ao falecimento de cônjuges homens, que possuem menor longevidade média.
Para o subgrupo de servidores públicos, essas probabilidades brutas por idade sofrem muita variabilidade em idades extremas, devido ao menor tamanho amostral. Por exemplo, se entre servidores de 25 anos houve poucos casos casados na amostra, a taxa poderia sair artificialmente baixa.
Para obter uma tábua mais confiável, aplicou-se um modelo de credibilidade Bühlmann-Straub (Bühlmann; Straub, 1970) combinando a experiência dos servidores com a da população geral. Em essência, assume-se que a curva de proporção casados dos servidores difere da geral por um deslocamento (shift) aproximadamente constante em certas faixas etárias. De fato, ao analisar os dados se identificou um pequeno diferencial: servidores do sexo masculino apresentam taxa de casamento ligeiramente superior à média (+1,55 ponto percentual), enquanto servidoras femininas exibem taxa ligeiramente inferior à média da população (-0,64 p.p.). Com base nisso, para idades com pouca representatividade de servidores (<30), ajusta-se a curva geral adicionando Δ (esses diferenciais) e então calcula-se uma combinação credível:
onde n_serv,x é o tamanho amostral (ponderado) de servidores na idade x e k é um parâmetro relacionado à variância. No projeto, adotou-se k como a raiz do número de médio de servidores. A proporção final credível fica
Com poucas observações, n pequeno, tipicamente em idades extremas, Z será baixo e a estimativa puxará mais para a curva geral ajustada; com muitos dados n grande, idades medianas, Z fica alto e preserva-se mais a experiência específica dos servidores Após essa etapa, aplica-se uma suavização por média móvel ponderada para eliminar serrilhados restantes. Utilizou-se uma janela de 5 anos e realizou-se 3 iterações, combinando a curva suavizada parcialmente com 30% da curva geral para ancorar as extremidades. Esse procedimento de graduação segue princípios atuariais clássicos (Spencer, 1904) para garantir que a tábua final de conjugalidade seja monótona e bem-comportada, sem flutuações irregulares, tornando-a apropriada para uso atuarial. O resultado é uma tábua de probabilidades de possuir cônjuge por idade P₍c₎(x), diferenciada por sexo, específica para servidores, mas fundamentada em dados populacionais nacionais, preenchendo uma lacuna importante, já que tábuas conjugais publicadas geralmente refletem outras populações.
Diferença de idade entre cônjuges (age gap)
De posse da probabilidade de existência de cônjuge em cada idade, o próximo passo é modelar a diferença de idade entre os cônjuges, variável crucial para projeção de pensão por morte. Em planos previdenciários, costuma-se adotar uma hipótese simplificadora, por exemplo, “esposas são 4 anos mais jovens que os maridos”, para estimar a expectativa de vida do cônjuge dependente.
Contudo, a realidade apresenta uma distribuição de diferenças de idade (age gap) mais complexa. Usando os microdados da PNAD, o projeto extraiu, para cada casal identificado (pessoa de referência do domicílio e seu cônjuge), a diferença de idade.
Por convenção, um age gap positivo indica que o participante (referência) é mais velho que seu cônjuge; negativo indica cônjuge mais velho. Em nossa sociedade, é mais comum maridos serem mais velhos que as esposas, resultando em age gaps positivos na maioria dos casos.
No grupo de servidores analisado, verificou-se, por exemplo, que um servidor homem de 60 anos tem em média uma esposa cerca de 5 anos mais jovem, ou seja, age gap médio de +5 anos; já uma servidora mulher de 60 anos tende a ter marido ligeiramente mais velho ou de idade próxima, resultando em age gap médio próximo de -1 ano, ou seja, marido ~1 ano mais velho. Esses valores médios, entretanto, variam conforme a idade do participante. O projeto calculou o age gap médio condicionado à idade do participante e ao seu sexo, incorporando novamente um modelo de credibilidade para ajustar eventuais diferenças sistemáticas entre servidores e população geral.
Além da média, avaliou-se o desvio-padrão dessa diferença, pois a dispersão é relevante – alguns casais têm diferença de 10, 15 anos ou mais. Análises exploratórias compararam o ajuste da distribuição do age gap à uma curva Normal versus uma distribuição t-Student, dado que esta última possui caudas mais pesadas e poderia capturar a incidência de casos com grande diferença de idade. Ao final, optou-se por usar t-Student com cinco graus de liberdade, porém, com truncamento da idade do cônjuge entre 15 e 100 anos, para que não fossem gerados números absurdos, já que a distribuição é ilimitada.
A abordagem por distribuição permite calcular de forma acurada a expectativa de vida remanescente do cônjuge usando tábuas biométricas, em vez de supor um diferencial fixo arbitrário para todas as idades. Além disso, o modelo de age gap alimenta simulações Monte Carlo no projeto: é possível sortear diferenças de idade conforme a distribuição observada para propagar incerteza nos cálculos, por exemplo, gerar cenários de cônjuge muito mais jovem ou mais velho e ver impacto no encargo.
Filhos dependentes
Filhos dependentes influenciam o custo da pensão por morte e, portanto, são importantes no modelo. Adotamos elegibilidade até 24 anos e, com base na PNADC 2023, identificamos convivência e idades; assim, considera-se dependente quem tem ≤24 anos no domicílio. Além disso, a PNAD não distingue biológicos de enteados; logo, ambos contam como filhos.
Estimamos, por idade e sexo do participante, (1) a probabilidade de ter ≥1 dependente, (2) o número médio de dependentes condicionado à existência, (3) a idade média do caçula e (4) o desvio-padrão das idades. Desse modo, capturamos não apenas a presença, mas também a estrutura etária.
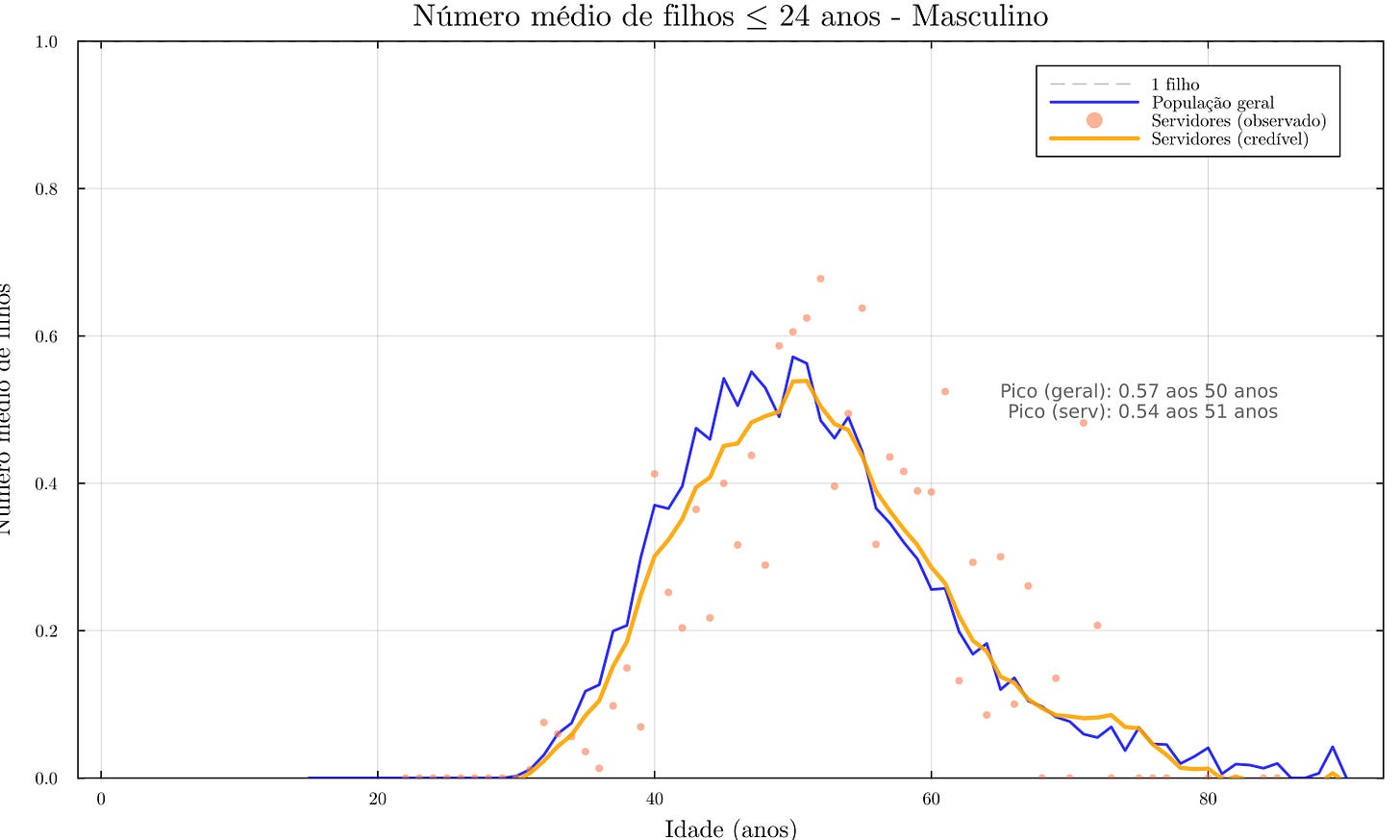
Os padrões para ter pelo menos um filho dependente seguem a intuição demográfica: a probabilidade atinge pico entre 30 e 40 anos: para homens em torno dos 40, supera 60%. Após os 50, inicia-se queda contínua; antes dos 25, permanece baixa; e após os 60, torna-se praticamente nula. Entre os que possuem dependentes, o número médio é ≈2 filhos, embora haja dispersão relevante (casos com 1 e também com 3 ou mais).
Em seguida, nas simulações sorteiam-se presença, quantidade e idades conforme distribuições condicionais (por exemplo, aos 35 anos: ~40% nenhum, ~30% um, ~20% dois, ~10% três+; valores ilustrativos). Para o cálculo atuarial, priorizamos o filho mais novo; consequentemente, a duração do benefício por filhos vai até ele completar 24 anos, ao passo que os demais cessam antes. Com base nisso, extraímos, por idade do participante, a distribuição da idade do caçula (ex.: aos 45 anos, tipicamente 10–15 anos). Ademais, aplicou-se credibilidade apenas residual entre servidores e população geral.
Dessa forma, obtemos uma tábua que, para morte aos x anos, fornece a probabilidade de deixar filhos, sua quantidade esperada e a duração estimada das pensões, que é insumo direto para encargo e reserva que calcularemos ao final. Abaixo, um exemplo de gráfico dessa análise. Outros gráficos podem ser consultados diretamente no repositório do projeto.
Encargo atuarial de pensão por morte (função heritor)
Com as etapas anteriores, conseguimos montar um panorama completo do possível grupo de dependentes de um participante que venha a falecer em determinada idade: se terá cônjuge e qual a idade deste, se terá filhos menores e quantos/quantos anos terão.
A função heritor então calcula o encargo atuarial condicional à morte nessa idade, ou seja, o valor presente esperado do fluxo de pensões que serão pagas aos dependentes dado que o participante falece na idade x.
Esse encargo é expresso em anos de benefício para facilitar a interpretação. Em outras palavras, em vez de dar o valor monetário exato (que depende do salário ou benefício do participante), expressa-se o custo como um múltiplo do benefício anual. Por exemplo, um encargo de 9,8 anos significa que o valor presente total das pensões a serem pagas equivale a 9,8 vezes o benefício anual do participante falecido. Para converter isso em moeda, bastaria multiplicar pelos valores de benefício anual (BEN) em reais: Custo (R$) = Encargo (anos) × BEN (R$/ano).
Cálculo: O encargo atuarial é composto de duas partes principais: pensão ao cônjuge e pensões aos filhos dependentes, que dependem da presença ou não de tais dependentes. Matematicamente, podemos descrever:
Se o participante era casado no óbito: será devida uma anuidade vitalícia ao cônjuge, ou seja, um benefício pago enquanto o cônjuge sobrevivente estiver vivo. O valor presente atuarial dessa anuidade equivale a ä₍y₎, onde y é a idade do cônjuge no óbito. Formalmente,
\(\ddot{a}_{y} = \sum_{t=0}^{\infty} v^{t}\, {}_{t}p_{y} \)representando a soma dos fatores de desconto multiplicados pela probabilidade de sobrevivência do cônjuge por T anos.
Em termos práticos, essa anuidade é aproximadamente a expectativa de vida remanescente do cônjuge em anos, porém ajustada pela taxa de desconto. No projeto, foi assumida uma taxa de desconto i = 6% ao ano
A tábua de mortalidade utilizada para os cônjuges (e participantes) foi a AT-2012 Basic Individual Annuity Mortality (SOA, 2012), com segregação por sexo.
Se o participante tinha filhos dependentes elegíveis: para cada filho haverá uma anuidade temporária até o filho atingir 24 anos. O valor presente de uma pensão temporária que começa na idade atual do filho z e cessa em n anos (quando ele faria 24) é dado por:
\(\ddot{a}_{z:\overline{n}\,|} = \sum_{t=0}^{n-1} v^{t}\, {}_{t}p_{z} \)onde n = 24 - z, que é o tempo restante até perder elegibilidade. Na prática, considera-se que crianças e jovens quase sempre sobrevivem ao período curto analisado. Assim, o fator que resume os pagamentos anuais fica muito próximo da própria duração do benefício. Com taxa de desconto anual de seis por cento, um filho de dez anos (catorze anos restantes) gera fator em torno de onze; já um filho de vinte anos (quatro anos restantes) gera fator perto de quatro. Portanto, quanto mais novo o filho, maior o encargo, pois os pagamentos se estendem por mais tempo.
Percentual de pensão: adotou-se a regra introduzida na legislação brasileira a partir de 2015. Desde 2015 (Brasil, 2015), a pensão por morte é calculada como 50% do benefício básico + 10% por dependente (cônjuge e filhos), limitada a 100%. Sem dependentes: 0%; um dependente: 60%; dois: 70%; … cinco ou mais: 100%. A cota familiar de 50% é compartilhada entre os beneficiários, e cada dependente adiciona 10% próprio. Atuariamente, o valor presente soma parcelas de cônjuge e filhos ponderadas por esses percentuais.
Em termos práticos para o cálculo atuarial, o valor presente das pensões deve somar as parcelas de cônjuge e filhos ponderadas por esses percentuais. O projeto calcula isso explicitamente via simulação Monte Carlo: para cada idade x do participante (de 30 a 80 anos analisada), simula-se um grande número de cenários consistentes com as probabilidades estimadas, sorteia-se se o participante tem cônjuge e filhos e quais as idades correspondentes. Para cada cenário simulado de composição familiar no óbito, calcula-se o valor presente das pensões:
Se não há dependentes, VP = 0;
Se há cônjuge e/ou filhos, aplica-se a fórmula de percentual para obter % do benefício a pagar; depois calcula-se VP = % × (valor presente da anuidade cônjuge + valor presente das anuidades temporárias de cada filho).
Nesse cálculo, quando há múltiplos dependentes, considera-se que o pagamento cessa proporcionalmente quando cada filho perde elegibilidade – por exemplo, se cônjuge + 1 filho recebem 70% juntos, quando o filho atingir 24 anos a pensão dele cessa e o cônjuge passaria a receber apenas 60% (a cota do filho não reverte). Assim, o fluxo de pagamento ao longo do tempo é modelado com um patamar menor após cada filho sair, seguindo a regra de não reversão das cotas (Brasil, 2015). A simulação captura essas dinâmicas individuais. Repetindo milhares de vezes, obtém-se uma distribuição do encargo atuarial Hx para idade x.
Os resultados para o encargo atuarial ou função de heritor mostram tendências intuitivas. Para idades jovens, o encargo médio é relativamente baixo, pois apesar de um eventual óbito jovem gerar pensão por muitos anos (cônjuge jovem e filhos pequenos poderiam receber por décadas), a maioria dos jovens não tem dependentes – o que puxa a média para baixo.
Em torno dos 30–40 anos, o encargo esperado cresce rapidamente, alcançando seu pico em faixas de meia-idade. Isso ocorre porque nesta fase muitos participantes têm tanto cônjuge quanto filhos pequenos simultaneamente, constituindo o cenário de maior custo.
Conforme a idade do participante aumenta além dos 50–60 anos, o encargo esperado diminui gradualmente: embora seja quase certo que haja um cônjuge dependente, os filhos já não são elegíveis (todos adultos), reduzindo bastante o custo, e o cônjuge do participante idoso também já terá idade avançada – o que reduz a duração esperada da pensão conjugal. Em idades extremas, próximas à longevidade limite, o encargo tende a zero, pois ou o participante não deixa ninguém (cônjuge já falecido, nenhum outro dependente) ou deixa um cônjuge muito idoso cuja expectativa de vida é baixa.
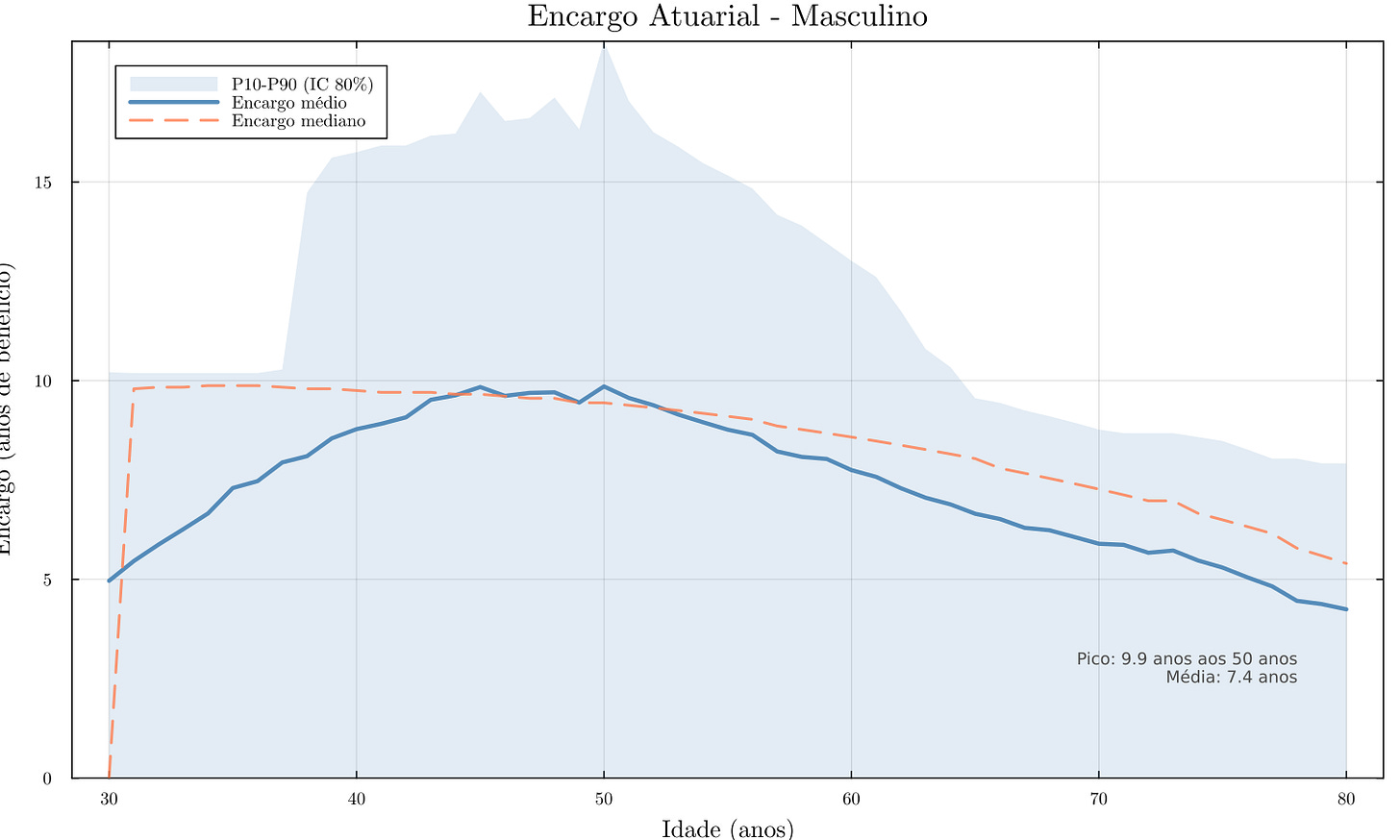
Os gráficos acima ilustram essas tendências. Para participantes masculinos, o encargo médio atinge valores em torno de 8–10 anos de benefício no pico, que ocorre aproximadamente entre 40 e 50 anos de idade (por exemplo, pode-se notar no gráfico que o pico ~9 anos ocorre aos ~45 anos, dependendo do resultado exato) – depois cai para cerca de 4 anos ou menos aos 80 anos.
Já para femininos, o encargo médio máximo é menor, em torno de 6–8 anos no pico, e declina para perto de 2 anos ou menos aos 80. Essa diferença reflete o fato de que homens tendem a deixar esposas mais jovens e que receberão pensão por mais tempo, aumentando o custo e frequentemente têm filhos menores quando morrem em meia-idade; além disso, virtualmente todos os homens casados deixarão uma viúva, enquanto muitas mulheres idosas não deixam viúvo (já eram viúvas elas próprias).
No conjunto, o encargo médio dos homens ao longo de 30–80 anos ficou cerca de 0,5–1 ano de benefício maior que o das mulheres (diferença média de aproximadamente 0,7 ano, pelas simulações) – confirmando a necessidade de separar por sexo.
A banda P10–P90 dos gráficos mostra a variabilidade: em idades onde o encargo médio é alto, também há enorme dispersão. Por exemplo, para homens em ~45 anos, o percentil 10% do encargo é próximo de 0 (casos de participantes sem dependentes nenhum, que não geram custo) enquanto o percentil 90% pode chegar a 15 anos de benefício ou mais (casos de participante com esposa jovem e vários filhos pequenos, gerando pensão máxima por longos períodos). Essa amplitude diminui em idades altas, onde cenários de muitos dependentes não ocorrem.
Também foi gerado um gráfico comparando diretamente as curvas de encargo médio de homens e mulheres em um mesmo painel, evidenciando que até cerca de 60 anos a curva masculina fica superior à feminina em 1–2 anos de benefício, mas após os ~70 anos ambas convergem a valores baixos (as mulheres ultrapassam ligeiramente os homens em encargo >75 anos, mas em níveis muito baixos, <1 ano, dado que algumas poucas ainda podem ter esposo vivo naquela idade).
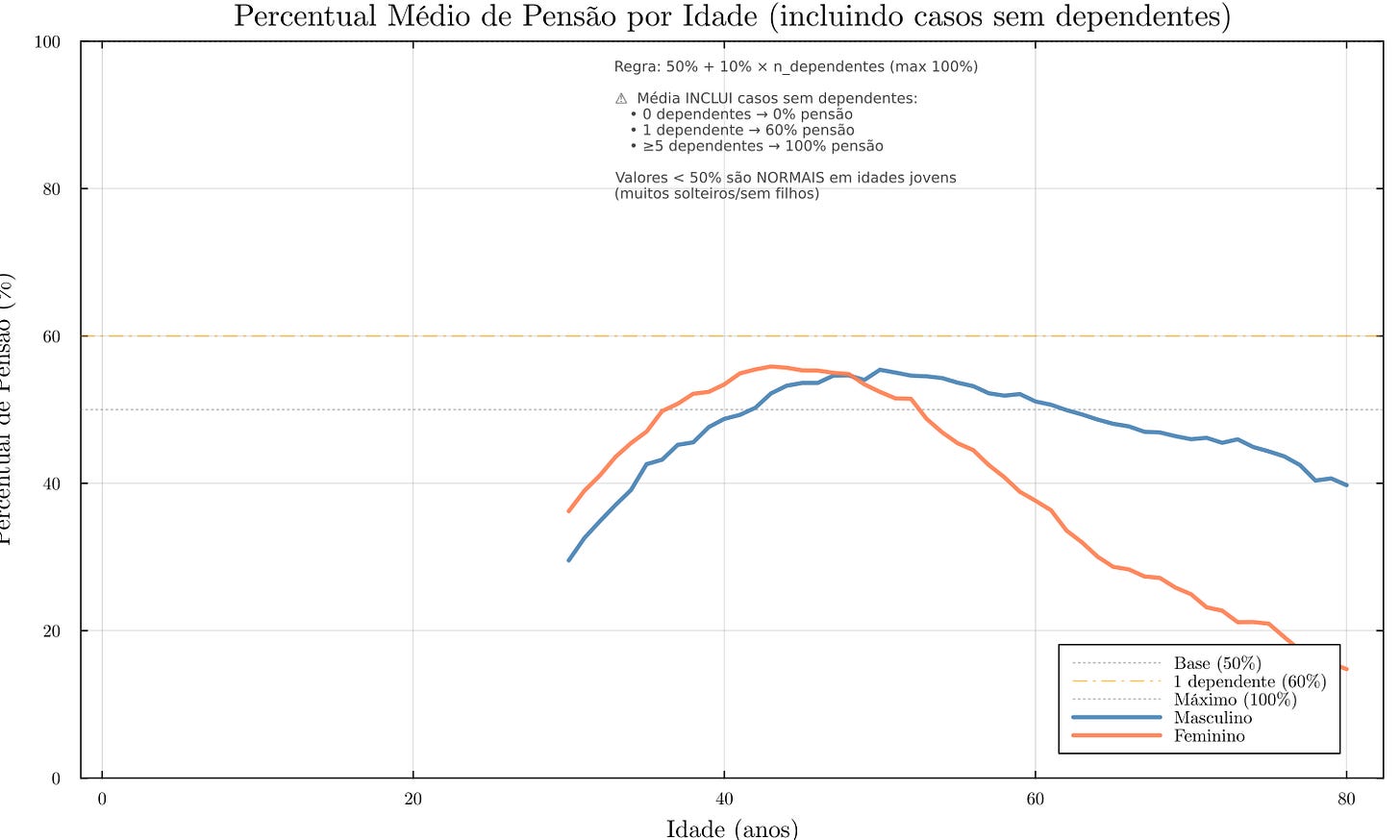
Outro resultado interessante do modelo é o percentual médio de pensão por idade, ou seja, qual fração do benefício seria paga em média considerando a chance de não ter dependentes. O projeto apurou que em idades jovens (20 e poucos anos), esse percentual médio fica abaixo de 20%, pois a maioria dos falecimentos nessa faixa não geraria pensão (por falta de dependentes).
O valor sobe rapidamente conforme aumenta a proporção de pessoas casadas/ com filhos: por volta de 40 anos, o percentual médio de pensão já ultrapassa 60%. Em idades próximas à aposentadoria (60 anos), o percentual médio se estabiliza em torno de 60–70% para homens (a maioria casados, recebendo pelo menos 60%), e cerca de 50–60% para mulheres (uma parcela significativa não deixa cônjuge). Em idades muito altas (>80), o percentual médio para mulheres chega a cair abaixo de 50% novamente, pois muitas não têm dependente sobrevivente. Esses valores abaixo de 50% podem ocorrer sem contradição com a fórmula porque incluem o caso de zero dependentes (pensão 0%) na média.
Por fim, avaliou-se a sensibilidade do encargo à taxa de juros atuarial. Juros mais baixos aumentam o valor presente das rendas futuras, encarecendo o encargo (e vice-versa). O projeto simulou o encargo médio em diferentes taxas (por exemplo, 4%, 6%, 8%) para algumas idades representativas (digamos 30, 50, 70 anos). Observou-se que reduzir a taxa de desconto de 6% para 4% a.a. pode elevar o encargo em torno de 15–25%, dependendo da idade – o impacto é maior para mortes jovens (encargos mais longos). Isso reforça que a premissa de juros é crucial na avaliação de reservas e deve ser escolhida conforme o regime financeiro do plano.
Reserva matemática para pensão por morte
Enquanto o encargo atuarial Hx calculado acima é um valor condicional (custo dado o falecimento na idade x), do ponto de vista da reserva técnica de um plano previdenciário precisamos do valor incondicional esperado do benefício por morte, dado que o participante está vivo na idade x. Em outras palavras, a reserva, ou provisão matemática, R(x), associada à cobertura de pensão por morte para um participante de x anos é a esperança do valor presente de todas as pensões futuras que serão pagas em caso de morte, considerando a incerteza de quando ele irá falecer. Atuariamente, essa reserva corresponde ao prêmio puro de um seguro de morte embutido no plano na idade x. Matematicamente, pode-se expressar:
onde tPx é a probabilidade do participante sobreviver de x até x+t, q(x+t) é a probabilidade de morte no intervalo (x+t, x+t+1], e H(x+t) é o encargo (valor condicional) se a morte ocorrer nessa idade futura. Essa fórmula nada mais é do que a aplicação do princípio do valor presente esperado, integrando sobre todas as idades possíveis de falecimento.
Intuitivamente, R(x) é muito menor que H(x) para idades x onde a pessoa tem muita vida pela frente, pois a morte pode não ocorrer senão muito mais tarde, ou pode ocorrer bem mais tarde quando o encargo será menor.
O projeto calcula R(x) utilizando a tábua de mortalidade AT-2012 mencionada. Como E(x+t) já foi pré-calculado na faixa de idades (30–80), a integração é realizada numericamente somando cada parcela anual de probabilidade de morte vezes encargo descontado.
Os resultados para a Reserva Matemática confirmam que ela é bem mais baixa que os encargos condicionais. Enquanto o encargo condicional variava na faixa de ~5 a 10 anos de benefício para idades ativas, a reserva típica para um participante ainda vivo fica da ordem de 0,2 a 0,8 anos de benefício apenas. Em outras palavras, em valor presente a companhia precisa reservar menos de 1 ano de benefício, durante a vida ativa do participante, para cobrir o risco de pensão por morte, o que faz sentido, pois a probabilidade de morte em cada ano é pequena.
Note que essa conclusão é específica para a tábua AT-2012 IAM Basic, o resultado pode variar se considerarmos outras tábuas e outras taxas de desconto. A tábua AT-2012 IAM Basic é considerada conservadora para fundos de pensão no Brasil, por ter expectativas de vida maior, por outro lado, há menos falecimentos em idade ativa, quanto o encargo de pensão é alto e, por conseguinte, isso reduz a reserva necessária para a pensão por morte.
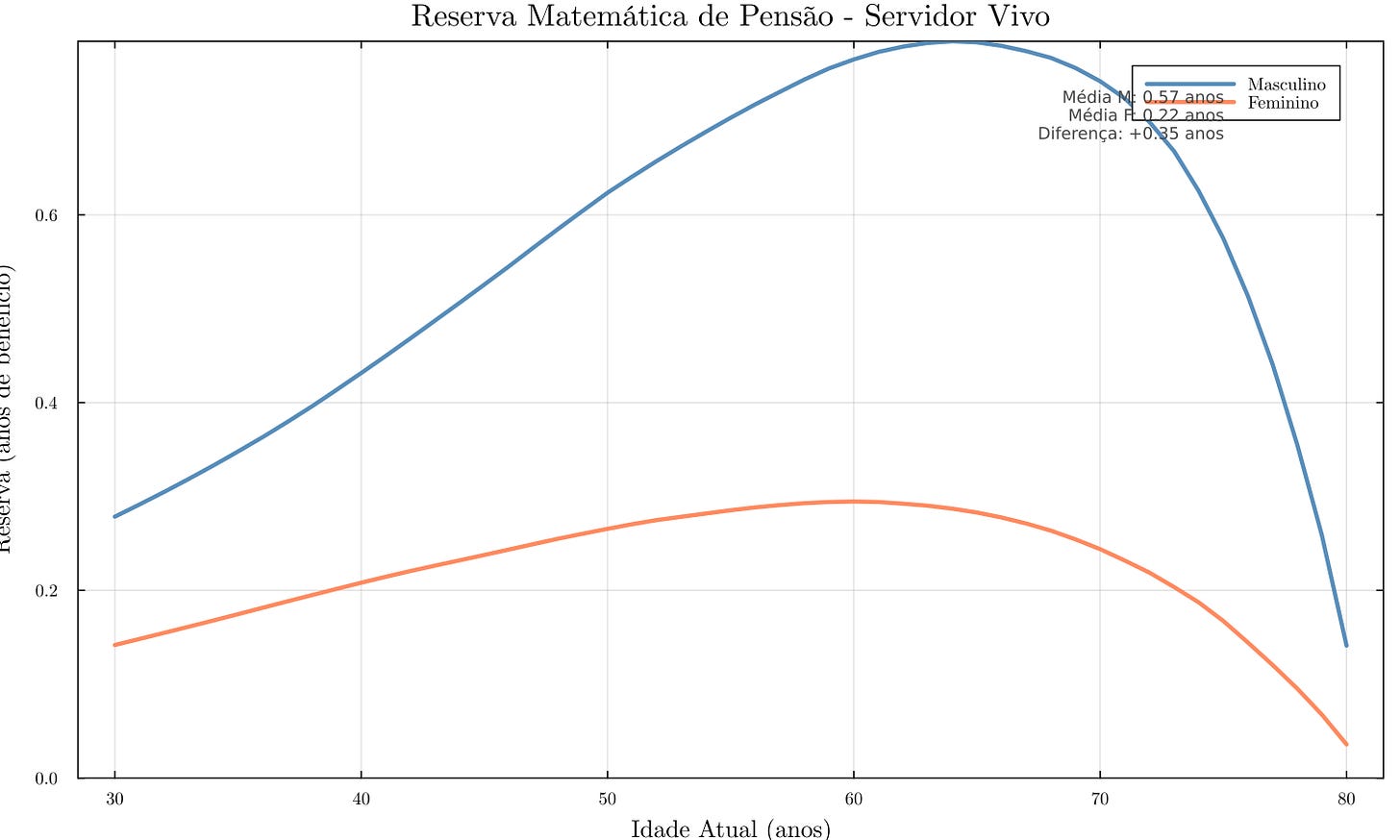
A figura abaixo apresenta a reserva por idade atual comparada entre sexos:
A reserva cresce com a idade no início, atinge pico por volta dos 50 e poucos anos e, depois, declina nas idades muito avançadas. O pico ocorre onde probabilidade de morte × encargo é máximo. Em idades jovens, a probabilidade de morte é muito baixa e, portanto, a reserva é pequena; na meia-idade, probabilidade já não desprezível e encargo elevado produzem o máximo; após 60–70, embora a mortalidade suba, o encargo cai (menos filhos e cônjuge mais velho), e o valor esperado recua. Além disso, o desconto temporal reduz contribuições de eventos distantes. No gráfico, a reserva máxima é cerca de 0,7–0,8 ano de benefício para homens e 0,5–0,6 para mulheres, ambos por volta dos 50; acima de 80, aproxima-se de zero.
Comparando sexos, apesar da maior longevidade feminina, a reserva masculina é maior na vida ativa, principalmente pela maior probabilidade de deixar dependentes, em especial viúvas mais jovens. Em média, excede a feminina em cerca de 0,1–0,2 ano; ao fim da vida laboral (por volta dos 60), ambas já ficam abaixo de 0,5 ano.
Medidas auxiliares ajudam a interpretar: a reserva equivale a pequena fração da expectativa de vida remanescente (na ordem de 2–4% no caso avaliado), indicando custo relativo modesto do benefício por morte em um plano BD típico. Outro resultado mostra a probabilidade de eventualmente deixar ao menos um dependente: embora um jovem solteiro de 25 anos raramente tenha dependentes hoje, sua probabilidade ao longo da vida de vir a falecer deixando alguém é bem maior (cerca de 40–50% para homens e 30–40% para mulheres), atingindo máximo entre 40–50 anos.
Em média de coorte, estima-se 60–70% para homens e 50–60% para mulheres, o que também implica chance não trivial de não deixar pensionista (30–40% homens; até 50% mulheres), reforçando o papel de regras que reduzem o benefício quando não há dependentes. Por fim, a comparação “Reserva vs Encargo” evidencia que a reserva é muito inferior ao encargo condicional em todas as idades, porque integra encargos futuros ponderados por mortalidade e descontados. Isso reflete: (1) baixa incidência de mortes em idades produtivas; (2) efeito dos juros no longo prazo; e (3) redução do encargo potencial conforme os filhos envelhecem e perdem elegibilidade.
Conclusão
O pq_heritor aplica dados demográficos atuais e técnicas atuariais para quantificar pensões por morte em planos BD: tábuas de conjugalidade e fecundidade da PNADC, credibilidade para subgrupos, premissas biométricas (AT-2012) e taxa de juros real de referência. Os resultados, expressos em anos de benefício, oferecem base objetiva para precificação, provisões e comunicação de riscos. Na prática, o risco de morte tem alto impacto em casos individuais, mas custo médio relativamente baixo ao plano. A abordagem pode ser atualizada com novas rodadas da PNADC e adaptada a mudanças regulatórias ou demográficas, mantendo transparência e rastreabilidade nas avaliações.
Referências
BRASIL. (2015). Medida Provisória nº 664/2014 convertida na Lei nº 13.135, de 17 de junho de 2015. Altera as regras de concessão da pensão por morte no RGPS. Diário Oficial da União, Brasília, DF, 18 jun. 2015.
BÜHLMANN, H.; STRAUB, E. (1970). Glaubwürdigkeit für Schadensätze. Mitteilungen der Vereinigung Schweizerischer Versicherungsmathematiker, 70.
SPENCER, J. (1904). On the Graduation of Rates of Sickness and Mortality. Journal of the Institute of Actuaries, 38(8), 334–343.
SOCIETY OF ACTUARIES (SOA). (2012). 2012 Individual Annuity Mortality Basic Table. Society of Actuaries, Schaumburg, IL.