Otimização de balanço bancário: um modelo prático de ALM para maximizar valor em um ambiente regulatório complexo
Maximizando EVA sob Basileia III — um “simulador de voo” para o balanço bancário
Introdução: o dilema do banqueiro moderno e a bússola da otimização
A gestão de uma instituição financeira é um exercício contínuo de equilíbrio sobre uma corda bamba. De um lado, reside a pressão incessante por rentabilidade para remunerar acionistas e reinvestir no negócio. Do outro, a necessidade imperativa de manter a solvência, a liquidez e a estabilidade, não apenas para a sobrevivência da própria instituição, mas para a saúde de todo o sistema financeiro. Este dilema fundamental, a tensão entre retorno e risco, foi drasticamente intensificado pela crise financeira global de 2008. Em resposta, reguladores em todo o mundo implementaram um arcabouço de regras mais rigoroso, notadamente o Acordo de Basileia III, que tornou a vivência neste ambiente ainda mais complexa e desafiadora.
Neste cenário, a Gestão de Ativos e Passivos, ou Asset-Liability Management (ALM), evoluiu de uma função de tesouraria para um pilar estratégico central. O ALM moderno não se limita a mitigar riscos; ele busca ativamente estruturar o balanço patrimonial de forma a otimizar o desempenho financeiro dentro de um apetite de risco predefinido e em conformidade com um denso emaranhado regulatório. Para enfrentar essa tarefa multifacetada, os bancos podem recorrer a modelos de otimização.
O modelo de otimização que será dissecado neste artigo serve como um "simulador de vôo" para o balanço de um banco. Ele permite que a gestão explore o vasto universo de decisões de alocação de ativos e captação de recursos, teste o impacto de diferentes estratégias e identifique uma estrutura "ótima". É crucial reconhecer que, como qualquer modelo, este é uma simplificação da realidade. A complexidade de um grande banco, com seus múltiplos produtos, geografias e fontes de risco, é imensa. No entanto, ao integrar de forma coesa as dimensões críticas de risco de capital, liquidez e taxa de juros, o modelo oferece uma representação notavelmente poderosa e prática dos principais dilemas enfrentados por um comitê de ativos e passivos (ALCO). Desenvolvido na linguagem de programação Julia, a implementação do modelo está disponível em → pq_alm_bancario.
Apresentação formal do modelo
O núcleo do problema de otimização consiste em maximizar uma função objetivo sujeita a um conjunto de restrições que refletem os limites operacionais, de risco e regulatórios. As variáveis de decisão são os vetores alocacao (representando os montantes investidos em cada classe de ativo) e funding (representando os montantes captados de cada fonte).
Função objetivo: maximização do valor econômico adicionado (EVA)
O objetivo é maximizar o EVA após impostos, definido como:
Restrições do modelo
O modelo opera sob as seguintes restrições:
(BAL) Equilíbrio do balanço: O total de ativos deve ser igual ao total de passivos mais o capital próprio.
\(\sum_i \text{alocacao}_i = \sum_j \text{funding}_j + \text{Capital Próprio} \)(CAP) Adequação de Capital: O capital próprio deve ser suficiente para cobrir os requerimentos de capital para os riscos de crédito, operacional e de mercado.
\(\text{Capital Próprio} \geq \text{Req}_{\text{Crédito}} + \text{Req}_{\text{Operacional}} + \text{Req}_{\text{Mercado}} \)(LCR) Cobertura de Liquidez de Curto Prazo: O estoque de ativos líquidos de alta qualidade (HQLA) mais as entradas de caixa (
inflows) deve ser maior ou igual às saídas de caixa (outflows) em um cenário de estresse de 30 dias.\(\sum_i (\text{alocacao}_i \times \text{fator HQLA}_i) + \text{Inflows} \geq \text{Outflows} \)(NSFR) Financiamento Estável Líquido: O montante de financiamento estável disponível (ASF) deve ser maior ou igual ao montante de financiamento estável requerido (RSF), multiplicado por um fator mínimo.
\(\begin{equation} \sum_j (F_j \times ASF_j) + (CP \times ASF_j) \geq \text{NSFR}_\text{mín} \times \sum_i (A_i \times RSF_i) \end{equation} \)(DUR) Gap de Duration: A diferença entre a duration ponderada dos ativos e a dos passivos deve permanecer dentro de limites predefinidos.
\(\begin{equation} \text{Limite}_{\min} \leq \frac{ \sum_i \text{alocacao}_i \times \text{dur}_i - \sum_j \text{funding}_j \times \text{dur}_j }{ \sum_i \text{alocacao}_i } \leq \text{Limite}_{\max} \end{equation} \)
Análise do modelo de otimização
Esta seção detalha o propósito e o impacto de cada componente do modelo apresentado formalmente.
O objetivo final: maximização do valor econômico adicionado (EVA)
A primeira e mais importante decisão na construção de um modelo de otimização é a definição de seu objetivo. Em vez de métricas contábeis tradicionais como o Lucro Líquido ou o Retorno sobre o Patrimônio (ROE), este modelo foi programado para maximizar o Valor Econômico Adicionado (EVA), também conhecido como Lucro Econômico.
A escolha é deliberada e profunda. O lucro contábil, embora amplamente utilizado, possui uma falha crítica: ele não considera adequadamente o custo de todo o capital utilizado para gerá-lo. Especificamente, enquanto o custo da dívida (juros) é uma despesa explícita na demonstração de resultados, o custo do capital próprio — a remuneração que os acionistas exigem pelo risco que assumem — é frequentemente ignorado na análise de desempenho operacional. O EVA corrige essa distorção. Uma empresa, incluindo um banco, só cria valor genuíno para seus acionistas quando seus retornos operacionais superam o custo de oportunidade de todo o capital investido, tanto de terceiros quanto próprio. Um banco pode apresentar lucro líquido positivo e, simultaneamente, destruir valor (EVA negativo) se sua rentabilidade não for suficiente para compensar seus acionistas pelo risco incorrido.
As amarras da realidade: as restrições regulatórias e de risco
Um banco não opera no vácuo. Suas decisões são limitadas por um conjunto de restrições que garantem sua solidez e a estabilidade do sistema.
(BAL) A Restrição de Equilíbrio do Balanço: Esta é a restrição mais fundamental, a identidade contábil que dita que o total de ativos deve ser igual à soma de passivos e patrimônio líquido. Ela garante que cada real alocado em ativos seja financiado por um real de passivos ou de capital próprio, impondo a lógica básica do balanço patrimonial.
(CAP) A Restrição de Adequação de Capital (Basileia III): Esta restrição implementa os requisitos de capital do Acordo de Basileia III, que exigem que um banco mantenha um nível mínimo de capital próprio para absorver perdas inesperadas. O capital é a principal defesa de um banco contra a insolvência. O modelo calcula o requerimento total de capital como a soma do capital necessário para cobrir riscos de crédito, operacional e de mercado. O capital é a "moeda" do risco em um banco. A restrição força o modelo a "pagar" por suas escolhas de investimento com este recurso escasso. Consequentemente, o modelo não pode simplesmente se concentrar nos ativos de maior retorno; ele deve encontrar um portfólio que gere o maior EVA por unidade de capital regulatório consumido. Esta dinâmica reflete o desafio do mundo real de otimizar o retorno ajustado ao risco sobre o capital (RAROC), um princípio central da regulação de Basileia III.
(LCR) A Restrição de Liquidez de Curto Prazo (Basileia III): Esta restrição implementa o Índice de Cobertura de Liquidez (LCR - Liquidity Coverage Ratio), uma das principais inovações de Basileia III, criada para evitar o tipo de crise de liquidez vista em 2008. O LCR exige que o banco mantenha um estoque de Ativos Líquidos de Alta Qualidade (HQLA) suficiente para cobrir suas saídas líquidas de caixa estimadas em um cenário de estresse severo de 30 dias. A restrição do LCR penaliza a dependência de fontes de financiamento instáveis e voláteis, conhecidas como "hot money". Isso força o modelo a priorizar fontes de captação estáveis e pulverizadas, mesmo que seu custo explícito seja marginalmente maior, conectando diretamente a estrutura de passivos à de ativos.
(NSFR) A Restrição de Financiamento Estável de Longo Prazo (Basileia III): Esta restrição implementa o Índice de Financiamento Estável Líquido (NSFR - Net Stable Funding Ratio), o complemento de longo prazo do LCR. Seu objetivo é garantir que o banco mantenha um perfil de financiamento estável ao longo de um horizonte de um ano, desincentivando o descasamento estrutural de prazos, como o financiamento de ativos de longo prazo com recursos de curto prazo. O NSFR atua como um freio estrutural, impedindo que o modelo financie sua carteira de crédito de longo prazo com recursos voláteis de curto prazo e forçando um alinhamento estratégico entre a maturidade dos ativos e a estabilidade dos passivos.
(DUR) A Restrição do Gap de Duration: Esta restrição gerencia a exposição do banco ao risco de taxa de juros, limitando o Duration Gap. A
duration é uma medida da sensibilidade do preço de um instrumento financeiro a variações nas taxas de juros. O Duration Gap é a diferença entre a duration ponderada dos ativos e a dos passivos. Um gap elevado indica que o valor econômico do patrimônio líquido do banco é altamente sensível a flutuações nas taxas de juros. Ao estabelecer um limite para este gap, a política de risco do banco efetivamente limita o tamanho da "aposta" direcional que ele pode fazer em relação às taxas de juros.
Premissas do modelo
O modelo opera dentro de um universo definido de possibilidades de investimento (ativos) e captação (passivos), além de parâmetros regulatórios e de custo. Estas premissas, explicitadas no código-fonte, representam as alavancas e as condições sob as quais o otimizador opera.
Tabela 1: Menu de ativos disponíveis (características e premissas)
Tabela 2: Fontes de captação disponíveis (características e premissas)
Parâmetros adicionais:
Capital próprio inicial: R$ 50.000.000
Custo de oportunidade do capital próprio: 15,0%
Requerimento mínimo de capital (Basileia): 11,5%
Requerimento mínimo de NSFR: 100%
Limite do gap de duration: -1,0 a +1,0 ano
A solução ótima: análise estratégica dos resultados
Com base nas premissas estabelecidas, o otimizador converge para uma única solução: o balanço que maximiza o EVA. A análise desta solução, detalhada no arquivo de resultados, revela a estratégia implícita do banco idealizado.
O balanço idealizado: estrutura de ativos e passivos
As tabelas a seguir apresentam a composição do balanço ótimo encontrado pelo modelo.
Tabela 3: Estrutura ótima de ativos
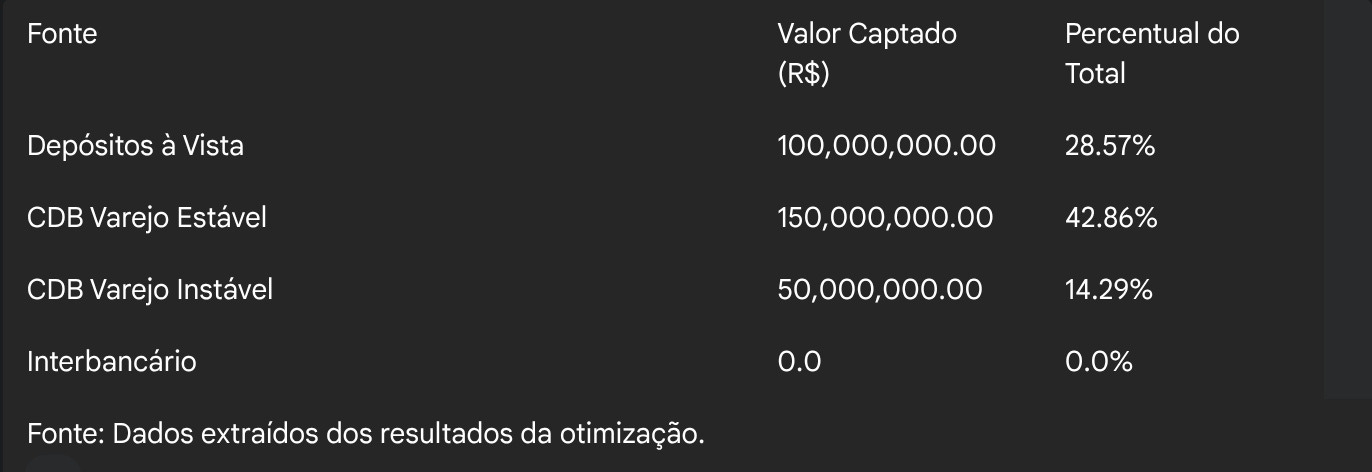
Tabela 4: Estrutura Ótima de Passivos (Funding)
A análise da estrutura revela duas decisões estratégicas claras. Primeiro, há uma dominância do Crédito Privado, que compõe mais de 75% da carteira de ativos. Isso ocorre porque seu retorno esperado de 18% é robusto o suficiente para compensar todas as suas desvantagens regulatórias e de risco. Segundo, o modelo utiliza integralmente as fontes de funding mais baratas e estáveis até seus limites máximos e evita completamente a captação Interbancária, uma consequência direta de seu tratamento punitivo pelas restrições de LCR e NSFR.
Painel de controle: métricas de desempenho e risco
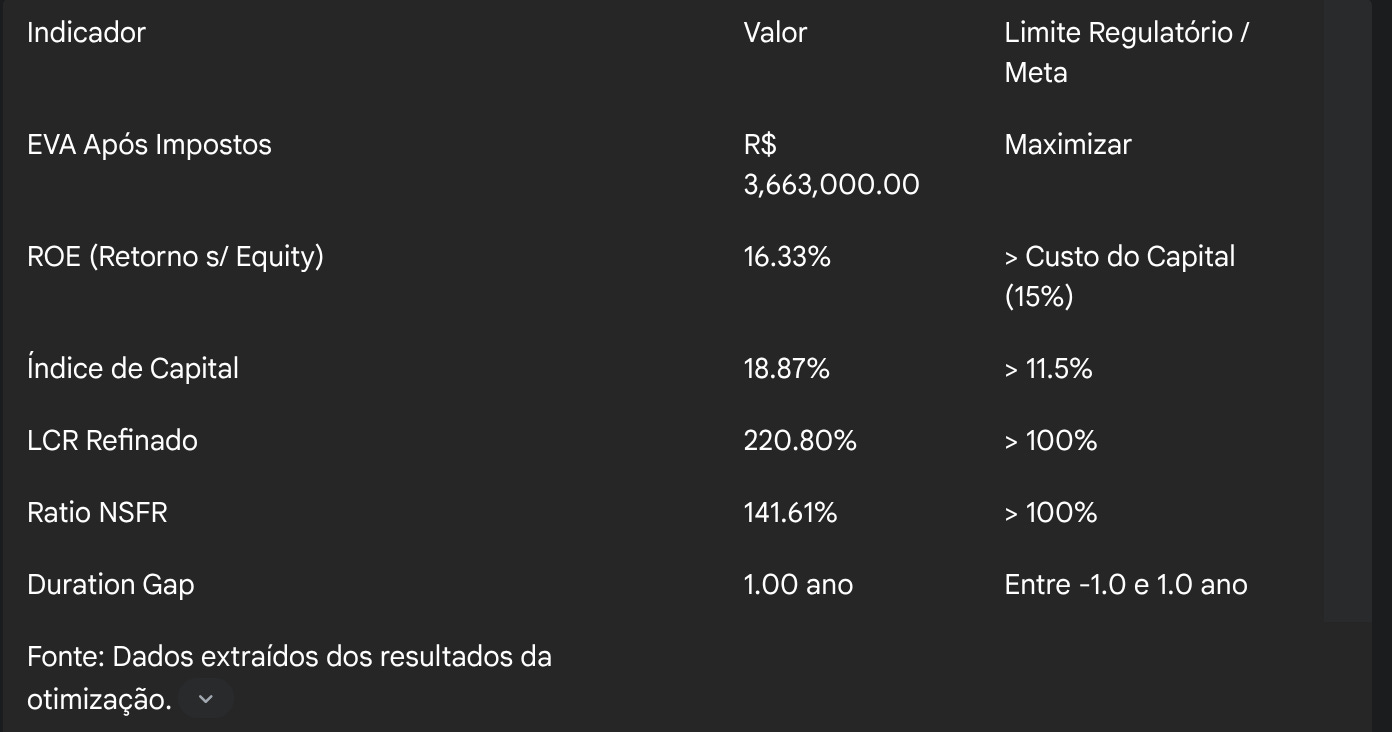
Tabela 5: Painel de controle da solução ótima (indicadores chave)
Uma análise mais atenta destes números revela uma estratégia que não é de aversão ao risco, mas de otimização do risco. O Duration Gap é de exatamente 1.00 ano, cravado no limite máximo permitido. Isso indica que o modelo está assumindo o máximo risco de taxa de juros permitido, pois considera que este é um risco bem remunerado que contribui para a maximização do EVA. Enquanto isso, os índices de liquidez (LCR e NSFR) e de capital estão confortavelmente acima de seus mínimos regulatórios. O modelo cumpre as regras, mas não aloca recursos excessivos para criar "gorduras" desnecessárias, pois isso seria caro e reduziria o EVA.
Conclusão: limitações do modelo e horizontes de expansão
Apesar de sua sofisticação, é fundamental reconhecer as limitações inerentes ao modelo apresentado e vislumbrar os caminhos para sua evolução. A jornada para um ALM verdadeiramente robusto não termina aqui; este modelo é um passo crucial, mas não o último.
As limitações de um mundo perfeito: determinismo e estágio único
O modelo, em sua forma atual, possui duas limitações conceituais importantes.
Primeiro, ele é determinístico. Isso significa que ele assume que todos os parâmetros de entrada — retornos, custos, fatores de risco, etc. — são conhecidos com certeza no momento da otimização. Ele encontra a melhor solução possível para uma única visão do futuro. No entanto, o mundo real é inerentemente incerto e estocástico.
Segundo, o modelo opera em um framework de estágio único. Ele otimiza o balanço para um único ponto no tempo, como uma fotografia. Ele não considera a natureza dinâmica e sequencial da gestão bancária, onde as decisões tomadas hoje afetam as opções disponíveis amanhã, e a estratégia deve ser reavaliada e ajustada continuamente em resposta a novas informações.
Rumo a um ALM mais realista: programação estocástica e modelos multiestágio
A superação dessas limitações aponta para metodologias de otimização mais avançadas, que representam a fronteira da prática de ALM.
A programação estocástica é o primeiro passo evolutivo. Em vez de usar estimativas pontuais para os parâmetros, um modelo estocástico utiliza uma "árvore de cenários" que representa um leque de futuros possíveis. O objetivo do otimizador muda: ele busca uma política de balanço inicial que seja robusta e tenha um bom desempenho em média, em toda a gama de futuros possíveis, conferindo resiliência à estratégia. O passo seguinte é a adoção de modelos multiestágio. Um modelo estocástico multiestágio captura a natureza sequencial da tomada de decisão. Ele permite que o modelo faça uma alocação inicial, observe um resultado do mercado, e então recalcule e ajuste a estratégia para o período seguinte. Isso espelha muito melhor o processo real de um ALCO, que não define uma estratégia imutável, mas sim um plano que é adaptado dinamicamente ao longo do tempo. Uma boa referência para essa abordagem é o livro ALM Modeling and Balance Sheet Optimization: A Mathematical Approach to Banking (The Moorad Choudhry Global Banking Series) (English Edition)
Em suma, o modelo determinístico e de estágio único apresentado neste artigo é uma ferramenta interessante para o planejamento estratégico. Ele fornece um "plano mestre" claro e de como seria um balanço ideal sob um conjunto central de premissas. Os modelos estocásticos e multiestágio, por sua vez, são ferramentas para a navegação dinâmica. A transição de um para o outro reflete a própria evolução da disciplina de ALM: de uma análise estática para uma gestão de risco dinâmica, preditiva e verdadeiramente estratégica.