Quando e como tornar as séries estacionárias para modelagem de machine learning (parte 1)
Transformações para estacionariedade: fundamentos, aplicações e implicações para modelos de previsão
A análise de séries temporais exige frequentemente que os dados sejam estacionários para que modelos de previsão funcionem adequadamente. Neste artigo, exploramos em profundidade o que é estacionariedade (em suas formas forte e fraca), por que ela importa para diferentes tipos de modelos (ARIMA, LSTM, XGBoost, Prophet etc.), e como transformar séries temporais não estacionárias – por meio de diferenças (simples e sazonais), transformações logarítmicas e Box-Cox – visando atender a esse requisito. Na segunda parte dessa série, também discutimos testes estatísticos (ADF, KPSS e outros) para diagnosticar estacionariedade e ilustramos um exemplo prático de automatização dessas transformações com o script apresentado na segunda parte dessa série. Por fim, como exemplo, apresentamos uma tabela com transformações selecionadas para séries reais de dados do IBGE e comentamos o impacto qualitativo dessas transformações na estabilidade e previsibilidade das séries.
Conceitos de estacionariedade em séries temporais
Em termos simples, uma série temporal estacionária é aquela cujas propriedades estatísticas não mudam ao longo do tempo. Isso significa, em geral, ausência de tendências de longo prazo, ausência de sazonalidades determinísticas e variância constante. No contexto formal, há dois principais tipos de estacionariedade:
Estacionariedade estrita (ou forte): Uma série Xt é estritamente estacionária se a distribuição conjunta de quaisquer instantes
for a mesma que a de
para qualquer defasagem h. Em outras palavras, todas as características estatísticas (de qualquer ordem) da série são invariantes no tempo. Essa definição é bastante restritiva; por exemplo, requer que não haja alteração em nenhum momento da distribuição, não apenas média e variância.
Estacionariedade fraca (ou de segunda ordem): Uma série é fracamente estacionária se apenas as primeiras duas momentâneas são constantes no tempo: i) a média E[Xt] é constante para todos t, e ii) a covariância Cov[Xt, Xt+k] depende apenas do intervalo k (e não do tempo absoluto). Na prática, assume-se também variância constante (que é o caso k=0 da covariância). Essa forma mais branda – também chamada covariance stationarity ou estacionariedade em segunda ordem – é a usual em econometria e aprendizado de máquina, pois muitos modelos só dependem de médias e covariâncias constantes ao longo do tempo. Vale notar que, para processos Gaussianos, estacionariedade fraca implica a forte, mas em geral a estacionariedade fraca é um critério separado.
Em resumo, uma série temporal estacionária (no sentido fraco) não possui tendência ou sazonalidade sistemática e tem variância estável. Por exemplo, um ruído branco é estacionário (média constante zero e variância constante), enquanto uma série com comportamento crescente ou com ciclos sazonais fixos não é estacionária a menos que essas características sejam removidas. Box & Jenkins destacam que, antes de modelar uma série, é preciso verificar se ela é aproximadamente estacionária – sem tendências, sazonalidades ou heterocedasticidade – e aplicar transformações se necessário.
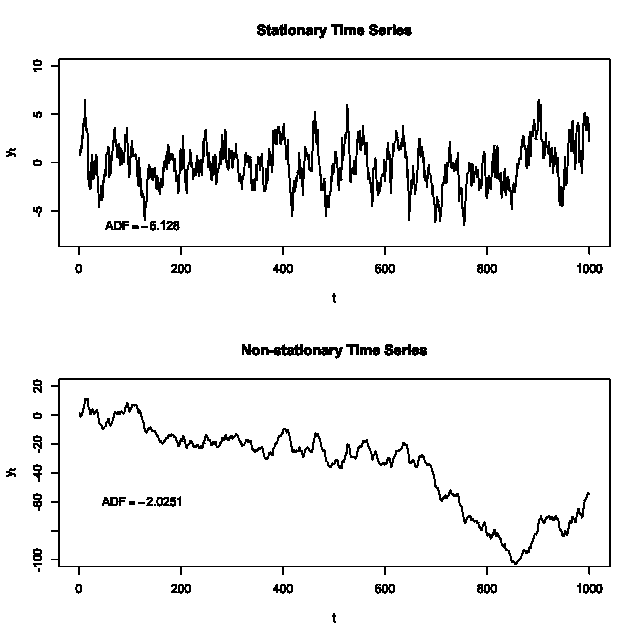
Figura 1: Comparação entre uma série estacionária (acima) e uma série não estacionária (abaixo). A série estacionária oscila em torno de uma média constante e variância aproximadamente constante, enquanto a série não estacionária apresenta uma tendência decrescente ao longo do tempo. Os valores do teste ADF (Augmented Dickey-Fuller) ilustrados indicam rejeição da hipótese de não-estacionariedade para a série de cima (ADF = -6.128) e falha em rejeitar para a série de baixo (ADF = -2.0251). Em termos práticos, isso significa que, no nível de 5% de significância, a primeira série pode ser considerada estacionária, ao contrário da segunda.
Por que a estacionariedade é importante?
Muitos métodos clássicos de previsão requerem ou assumem estacionariedade. Modelos da família ARIMA (Autoregressive Integrated Moving Average), por exemplo, são construídos sob a premissa de que os dados são estacionários após eventuais diferenciações. No procedimento de Box-Jenkins para ajuste de ARIMA, a primeira etapa é identificar quantas diferenças são necessárias para tornar a série aproximadamente estacionária. Sem estacionariedade, as propriedades estimadas pelo modelo (como coeficientes autoregressivos) não se mantêm no futuro, comprometendo a validade das previsões. Em suma, o componente “Integrado” (I) do ARIMA refere-se ao número de diferenciações aplicadas na série para remover a não-estacionariedade. Uma série com tendência ou sazonalidade não pode ser modelada diretamente por um ARMA puro; antes é preciso remover esses componentes (por exemplo, diferenciar uma vez para remover tendência linear.
Contudo, nem todos os modelos de previsão tratam a estacionariedade da mesma forma ou exigem transformações explícitas dos dados:
Modelos ARIMA e familiares: Conforme citado, ARIMA exige estacionaridade (após diferenciação). Por exemplo, um ARIMA(0,1,1) modela diferenças de primeira ordem da série original. Da mesma forma, modelos SARIMA exigem estacionaridade tanto na parte regular quanto na sazonal (aplicando diferenciação sazonal D além da diferença regular d. Se a série não for adequadamente estacionarizada (por exemplo, removendo tendência e sazonalidade), o ajuste de um ARIMA pode levar a resíduos autocorrelacionados e parâmetros instáveis.
Redes neurais recorrentes (RNN/LSTM): Modelos de aprendizado profundo, como LSTMs, teoricamente podem aprender padrões complexos inclusive em séries não estacionárias. Eles não exigem explicitamente que os dados sejam estacionários, pois podem incorporar tendências e sazonalidades como parte do padrão a ser aprendido. Por exemplo, diferentemente do ARIMA (linear), um LSTM pode em tese aprender uma relação não linear de longo prazo, capturando uma tendência exponencial ou um ciclo, desde que tenha dados suficientes. Estudos indicam que a noção de “estacionariedade” é menos rígida nesses modelos – LSTMs e GRUs conseguem aproveitar dependências de longo prazo e não linearidades, tornando-os mais robustos a certas formas de não-estacionariedade. Entretanto, na prática, mesmo redes neurais podem ter dificuldade se houver deriva constante: se os dados de teste tiverem distribuição muito diferente dos dados de treino (por exemplo, uma tendência leva os valores a patamares nunca vistos antes), o desempenho de generalização cai. Assim, muitas vezes é recomendável eliminar componentes sistemáticos (normalizar a série, remover tendência média ou estacionalidade) para facilitar o aprendizado e melhorar a estabilidade da rede, ainda que não seja uma exigência teórica estrita.
Modelos baseados em árvores (e.g. XGBoost): Algoritmos de machine learning tradicionais, como XGBoost, não têm pressupostos explícitos de estacionariedade porque não modelam diretamente a dependência temporal como uma regressão de valores passados contínua. Em abordagens de árvores para séries temporais, geralmente se incluem features como lags da série ou indicadores de tempo, e a árvore aprende divisões baseadas nesses preditores. Ainda que o modelo em si não exija estacionariedade, um conjunto de features derivadas mal selecionado pode sofrer se a distribuição dos valores muda drasticamente. Por exemplo, suponha que usamos valores defasados Y{t-1}, Y{t-12} como variáveis para prever Yt: se Yt tem uma forte tendência, os valores em períodos diferentes não serão comparáveis diretamente pelas árvores (precisariam, na prática, de divisões específicas por intervalos de tempo). Ao remover tendência e sazonalidade a priori, podemos obter features (como diferenças) mais informativas e que generalizam melhor. Em resumo, embora não haja uma suposição estatística de estacionariedade nos métodos de árvore, em cenários de previsão muitas vezes aplicamos transformações semelhantes (diferenças, etc.) para estabilizar o comportamento da série e facilitar o aprendizado do modelo.
Modelos estruturais/decomposição (Prophet, ETS): Abordagens como o Prophet (Facebook) ou os modelos clássicos de Suavização Exponencial (ETS) explicitamente modelam tendências e sazonalidades dentro do algoritmo. O Prophet, por exemplo, ajusta uma tendência (linear com saturação ou não linear) e componentes sazonais harmônicos aos dados, admitindo que a série observada Yt pode ser decomposta em Yt = g(t) + s(t) + h(t) + ruído(t), (onde g(t) é a tendência, s(t) a sazonalidade periódica, h(t) efeitos de feriados, e ruído(t) ruído) sem necessidade de tornar Yt estacionária previamente. Portanto, não é necessário diferenciar ou remover tendência antes de usar Prophet, pois o modelo a captura diretamente. De fato, se aplicarmos diferenças numa série que tem um componente de tendência que o Prophet poderia modelar, estaríamos “tirando” informação que o modelo espera aproveitar. Em outras palavras, stationarity não é pré-requisito para o Prophet, diferentemente de modelos como ARIMA. Entretanto, é importante entender que Prophet assume que a tendência g(t) é relativamente simples (por padrão, uma linha quebrada por pontos de mudança) e que s(t) é periódica estável – se houver padrões não estacionários mais complexos que não caibam nesses componentes (por exemplo, uma mudança abrupta de regime não informada como feriado), o desempenho pode degradar. Mas, em linhas gerais, modelos com componente de tendência embutido (Prophet, ETS) trabalham diretamente com séries não estacionárias (com crescimento, sazonalidade etc.), ao contrário dos modelos puramente baseados em dependência de lags (ARIMA, modelos de regressão linear) que requerem estacionaridade para funcionar corretamente.
Resumindo, modelos lineares de séries temporais requerem estacionariedade, enquanto modelos de machine learning e decomposição podem lidar com não-estacionariedade incorporando componentes explícitos ou aprendendo padrões complexos. Ainda assim, muitas vezes transformamos a série mesmo para modelos flexíveis, a fim de melhorar a aprendizagem ou satisfazer suposições dos métodos estatísticos. A chave é conhecer seu modelo: se ele supõe invariância estatística no tempo, é preciso tornar os dados estacionários; se não, pode-se optar por não diferenciar, mas ainda assim monitorar se há deriva entre treino e teste.
Transformações clássicas para tornar séries estacionárias
Várias transformações podem ser aplicadas para converter uma série não estacionária em estacionária. As transformações escolhidas dependem da natureza da não-estacionariedade presente (tendência determinística, raiz unitária, sazonalidade, variância não constante, etc.). A seguir, discutimos as técnicas mais comuns, critérios para usá-las e exemplos práticos de quando aplicá-las:
Diferenciação simples (Diferença de primeira ordem): Consiste em computar diff Yt = Yt - Y{t-1}. É a ferramenta fundamental para remover tendências de uma série. Se a série original apresenta um comportamento crescente ou decrescente ao longo do tempo (possui raiz unitária unitária de ordem 1), a primeira diferença muitas vezes resulta em uma série com média aproximadamente constante. Diferenciar elimina mudanças no nível da série, tornando-a estacionária em média ao reduzir ou eliminar tendências lineares. Por exemplo, se Yt segue aproximadamente uma tendência linear Yt ~ A + B * t, então diff Yt ~ B + ruído – ou seja, a diferença resulta em um valor oscilando em torno de B (que seria a inclinação média) ao invés de crescer indefinidamente. Em muitos casos, B será próxima de 0, tornando diff Yt aproximadamente com média zero. A Figura 1 acima ilustra este efeito: a série inferior (não estacionária) possui uma tendência que ao diferenciar seria removida.
Quando aplicar: sempre que a série apresentar tendência não estacionária (identificada por teste de raiz unitária como ADF, ou inspeção visual/ACF mostrando autocorrelação alta persistente). Critério prático: ACF que decai lentamente e PACF com pico significativo em lag 1 sugerem necessidade de primeira diferença. A aplicação de 1 diferença corresponde ao parâmetro d=1 nos modelos ARIMA.
Diferenciação sazonal: É uma extensão da ideia de diferenciação para remover padrões sazonais periódicos. Define-se diff[m] Yt = Yt - Y{t-m}, onde m é o período da sazonalidade (por exemplo, m=12 para dados mensais com sazonalidade anual). Essa operação elimina um componente sazonal determinístico estável, porque subtrai cada observação pelo valor do ciclo anterior equivalente. Por exemplo, se uma série possui picos todo mês de dezembro, a diferença sazonal m=12 fará com que Y{dez/2021} - Y{dez/2020} remova esse efeito periódico, ressaltando somente as mudanças ano a ano.
Quando aplicar: quando há evidências de sazonalidade regular – seja por inspeção gráfica (padrões repetitivos a cada ano, trimestre, semana etc.), seja por picos significativos nos autocorrelogramas nos múltiplos do período (pico em lag 12 no ACF, por exemplo). Hyndman recomenda aplicar a diferença sazonal antes da diferença regular quando a série apresenta um componente sazonal pronunciado (f0nzie.github.io). Na prática, frequentemente usamos Ds=1 (uma diferença sazonal) em modelos SARIMA para remover sazonalidade anual de séries mensais ou trimestrais. É importante notar que a diferenciação sazonal pode por si só resolver tanto a sazonalidade quanto uma possível tendência: por exemplo, uma série com tendência linear mais sazonalidade anual pode exigir tanto Ds=1 quanto d=1 (diferença sazonal e diferença regular adicionais). Devemos verificar a estacionariedade após a primeira diferenciação sazonal; se ainda houver tendência residual, aplica-se então a diferença regular. Diferenciar em excesso (por exemplo, usar Ds=1 e d=1 sem necessidade) deve ser evitado, pois adiciona ruído desnecessário.
Transformação logarítmica: Aplicar Yt´ = ln(Yt), sendo ln o log natural, é uma forma eficaz de estabilizar a variância de muitas séries econômicas. Séries cujo desvio-padrão cresce proporcionalmente ao nível (por exemplo, série de preços ou índices econômicos onde flutuações absolutas aumentam ao longo do tempo) têm comportamento multiplicativo. O log converte variações multiplicativas em aditivas. Por exemplo, uma série que cresce exponencialmente ou cujas oscilações percentuais são constantes se torna linear (ou com amplitude estabilizada) ao tomar o log. Hyndman observa que transformações como o log muitas vezes estabilizam a variância de uma série temporal (qiushiyan.github.io).
Quando aplicar: se a amplitude das flutuações da série aumenta com o nível da série. Um critério quantitativo pode ser verificar a relação entre a média e a variância móvel: séries multiplicativas apresentam variância crescente com a média. Outra dica é plotar Yt e ln(Yt) e ver se a segunda parece “menos heterocedástica”. Além disso, o teste de heterocedasticidade (como teste de Breusch-Pagan em resíduos ou métodos que checam a variância proporcional, que vamos discutir no próximo artigo desta série, pode indicar a necessidade de log. Importante: só é aplicável diretamente se todos os valores forem positivos. No caso de zeros ou valores negativos, pode-se adicionar uma constante antes do log ou então usar transformações do tipo Box-Cox. Muitas séries econômicas como PIB, índices de preços e produção industrial se beneficiam do log – após essa transformação, uma tendência exponencial vira aproximadamente linear (facilitando remoção com uma diferença) e a variabilidade relativa se torna aproximadamente constante.
Exemplo prático: Um índice de preços ao consumidor (IPC) acumulado geralmente cresce exponencialmente (5% ao ano de inflação implica multiplicação por 1,05 anual). Tomar log do índice de preços faz a série crescer linearmente (aproximadamente 0,05 por ano em log), e assim uma diferença no log fornece a taxa de inflação percentual, que costuma oscilar em torno de uma média estável. Nesse caso, aplicar log e depois diferença é preferível a apenas diferenciar o índice bruto (que resultaria numa série de incrementos absolutos, cuja variância tende a aumentar quando os preços absolutos aumentam).
Transformação Box-Cox: É uma generalização da transformação de potência que inclui o log como caso especial. Definida por
permite ajustar o parâmetro lambda para melhor estabilizar a variância ou aproximar a normalidade.
Quando aplicar: se a relação entre variância e nível não for claramente de forma logarítmica ou se a série contiver zeros/negativos (log não aplicável diretamente). O parâmetro lambda pode ser estimado por máxima verossimilhança ou minimizando a estatística de curtose, por exemplo. Em muitos casos, lambda próximo de 0 (log) já é suficiente, mas às vezes lambda=0,5 (raiz quadrada) é usado para volumes (ex: contagens de população), lambda = -1 para inverso, etc. O Box-Cox é útil como passo preliminar: por exemplo, séries de demanda de energia elétrica muitas vezes usam lambda ~ 0,3. Após escolhido lambda, procede-se com diferenças se ainda houver tendência/sazonalidade.
Detrendização por regressão: Embora a diferenciação seja a forma mais comum de remover tendências, outra abordagem é modelar a tendência explicitamente e subtraí-la. Por exemplo, ajustar uma regressão linear Yt = α + β * t aos dados e então trabalhar com os resíduos ε(t) = Yt - (α + β * t). Isso remove uma tendência linear determinística sem introduzir a dependência incremental causada pela diferença. Similarmente, poderia-se ajustar um modelo de regressão com termos polinomiais ou exponenciais se a tendência for não-linear.
Quando aplicar: se acredita-se que a tendência é determinística e de forma simples (linear, quadrática etc.) e se quisermos interpretar a tendência separadamente. Em muitos casos, diferenciar ou detrendar dão resultados similares quanto à estacionariedade dos resíduos, mas a regressão pode ser útil para extrapolar a tendência separadamente ou quando a diferença pode introduzir correlações negativas artificiais. O pacote
sktimeinclui, por exemplo, um transformador Detrender que realiza essa subtração de um modelo de tendência ajustado. No entanto, para propósitos de previsão automática (especialmente com ARIMA), a diferenciação é mais utilizada, pois ela efetivamente faz a detrendização de forma não-paramétrica.
Outras transformações: Em alguns casos, transformações como normalização (padronizar para média zero e variância um) são usadas para facilitar a modelagem, embora não tornem a série estacionária por si só. Elas podem ser úteis combinadas com log ou diferenciação. Para séries com sazonalidade multiplicativa, o uso conjunto de log e diferença sazonal costuma funcionar bem. Uma alternativa mais avançada é a diferenciação fracionária , que permite alcançar estacionariedade sem eliminar completamente a memória de longo prazo. Com 0 < d < 1, essa técnica suaviza a série preservando parte da autocorrelação, o que é útil em séries com long memory (ex: ativos financeiros ou indicadores macroeconômicos). Ela pode ser aplicada via expansões binomiais ou filtros como o método de Hosking, e está disponível em pacotes como fracdiff no python. É indicada quando há autocorrelação persistente, mas inferior a uma raiz unitária, e queremos modelos estacionários que mantenham parte das dependências de longo prazo. Já para séries com quebras estruturais, transformações simples não bastam. Nesses casos, técnicas de decomposição com variáveis de intervenção ou testes como Zivot-Andrews são mais adequadas. Em suma, nem toda não-estacionariedade se resolve com diferenças – o diagnóstico cuidadoso é essencial.
Em síntese, a escolha da transformação adequada depende do diagnóstico inicial da série. Exemplos práticos combinados: Uma série de produção industrial mensal geralmente exige log (para estabilizar variância), diferença sazonal (para remover o padrão anual) e possivelmente diferença adicional se houver tendência de crescimento. Já uma taxa de desemprego mensal (percentual) pode precisar apenas da diferença sazonal, caso oscile em torno de um valor médio sem tendência de longo prazo acentuada (após remover o efeito sazonal de contratação e dispensa típicos em determinados meses). Cada transformação deve ser avaliada por métricas estatísticas: inspeção do gráfico da série transformada, função de autocorrelação dos resíduos e testes formais de estacionariedade.
Ufa! Mas você sabe: pode ser que fazer esse tipo de análise de série em série seja absolutamente inviável! Estamos falando de machine learning e em um novo mundo com abundância de dados. Então, no próximo artigo, vamos falar sobre testes de estacionariedade e uma forma de automatizar essas transformações.
Até lá!