Podemos confiar na regra da raiz do tempo para escalar o risco?
Evidências do Ibovespa mostram que mesmo um expoente α≈0,5 pode esconder armadilhas em diferentes horizontes
Introdução
A regra de bolso que escala o VaR de 1 dia para horizontes maiores pela raiz do tempo (holding period)
só é válida quando retornos são independentes e identicamente distribuídos, com variância finita e sem memória temporal. Essa é a leitura browniana da dinâmica de preços, coerente com a hipótese de mercados eficientes em sua forma estatística (FAMA, 1970).
Na prática, séries financeiras apresentam caudas pesadas e volatilidade em clusters (CONT, 2001), o que pode distorcer substancialmente o escalonamento por raiz de h. (MANDELBROT, 1963; MCNEIL; FREY; EMBRECHTS, 2015). Uma alternativa mais aderente aos dados é estimar empiricamente um expoente de escala α via regressão log–log de log VaR(h) contra log(h), permitindo capturar desvios sistemáticos em relação a 0,5 (raiz quadrada).
Este artigo usa o código em Julia do repositório PQ Fractal Risk Scaling para analisar o Ibovespa (^BVSP) entre 2004-12-31 e 2024-12-31. Apresentamos a seguir como obter e como interpretar os resultados, e discutimos se um α≈0,5 obtido nos autoriza a escalar à vontade. A resposta curta é não: mesmo quando o α encontrado parece browniano, há armadilhas de amostra, curvatura por horizonte e mudança de regime que podem comprometer a cobertura do VaR ao extrapolar para janelas longas (KUPIEC, 1995; CHRISTOFFERSEN, 1998; MCNEIL; FREY; EMBRECHTS, 2015).
Como usar o repositório e o que esperar dos artefatos
O código do repositório organiza o fluxo em quatro blocos:
Construção de retornos e retornos agregados por horizonte;
curva VaR(h) empírica e regressão log–log para estimar α;
rolling α(t) com IC por bootstrap em blocos;
backtests de cobertura (Kupiec e, opcionalmente, Christoffersen) para comparar raiz de h com h elevado a α .
Ao executar o workflow para algum ticker específico, o repositório gera um diretório de saída contendo:
Resumo estatístico e parâmetros fractais: retorno e volatilidade, assimetria/curtose, α, IC e R2 e VaR(1);
curva VaR(h), com eixo log–log, por horizonte h, com as referências raiz de h e h elevado a α;
regressão log–log destacando a inclinação α, erro padrão e R2;
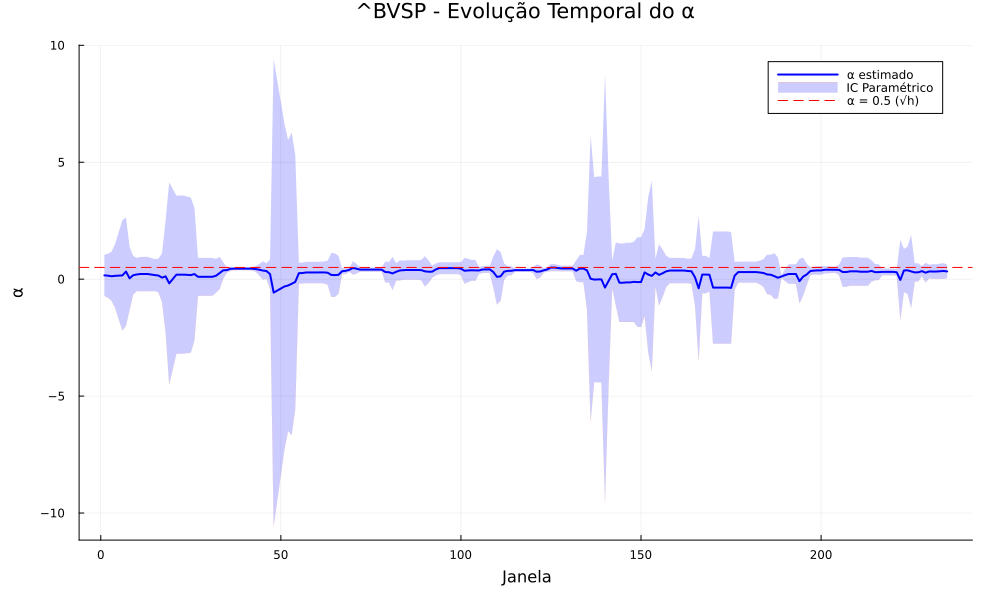
série temporal do rolling de α(t) com bandas de confiança bootstrap;
taxas de violação por horizonte nos backtests, com linha de referência a depender do nível de VaR utilizado..
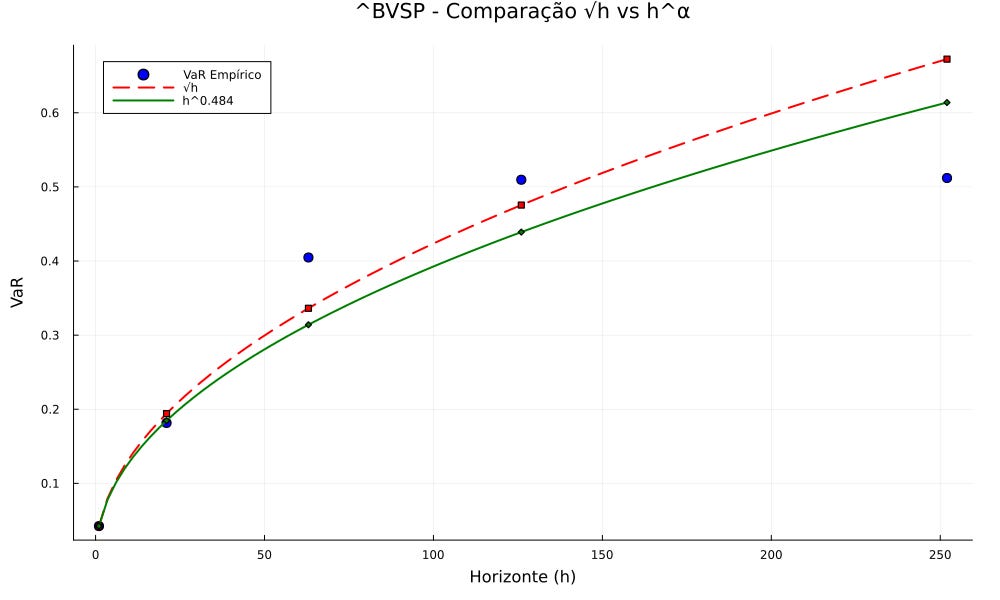
comparação das curvas VaR(h) empírico, raiz de h e h elevado a α.
resultados formais de Kupiec (e opcionalmente Christoffersen) por horizonte e por método.
Com esses artefatos, a leitura flui naturalmente: primeiro entende-se a escala média (α e qualidade do ajuste), depois inspeciona-se a estabilidade temporal (α(t)), e por fim verifica-se cobertura método a método.
O que mostram os dados do Ibovespa (2005–2024)
Nível, cauda e scaling médio
O resumo estatístico indica volatilidade diária de 1,67% (anualizada ≈26,6%) e curtose 9,37, sinal inequívoco de caudas pesadas — muito além do valor 3 da Normal.
O VaR diário empírico (99%) estimado foi de 4,24%. Na regressão log–log, o expoente fractal saiu α=0,4835 com erro padrão 0,0445 e R2=0,9752, fornecendo um ajuste excelente e compatível com um comportamento quase browniano. O IC 95% [0,3419;0,6251], porém, é largo o suficiente para acomodar desvios relevantes de 0,50 em subperíodos.
Interpretação: o scaling médio não contradiz a regra da raiz, mas a cauda é pesada; logo, convergência ao regime normal é lenta e o desempenho da regra da raiz pode deteriorar em certos horizontes ou regimes (MANDELBROT, 1963; MCNEIL; FREY; EMBRECHTS, 2015).
Essas figuras deixam visível a linearidade global e a inclinação próxima de 0,5, mas já antecipam pequenas discrepâncias por horizonte.
A estabilidade temporal de α
O rolling α(t) acrescenta a dimensão de tempo: mesmo quando a média histórica está perto de 0,50, janelas específicas podem mostrar persistência (α>0,5) ou antipersistência (α<0,5). Isso é coerente com a alternância de regimes de baixa e alta volatilidade documentada para mercados emergentes (CONT, 2001) e com a literatura de rough volatility que identifica rugosidade intensa em escalas curtas (GATHERAL; JAISSON; ROSENBAUM, 2018).
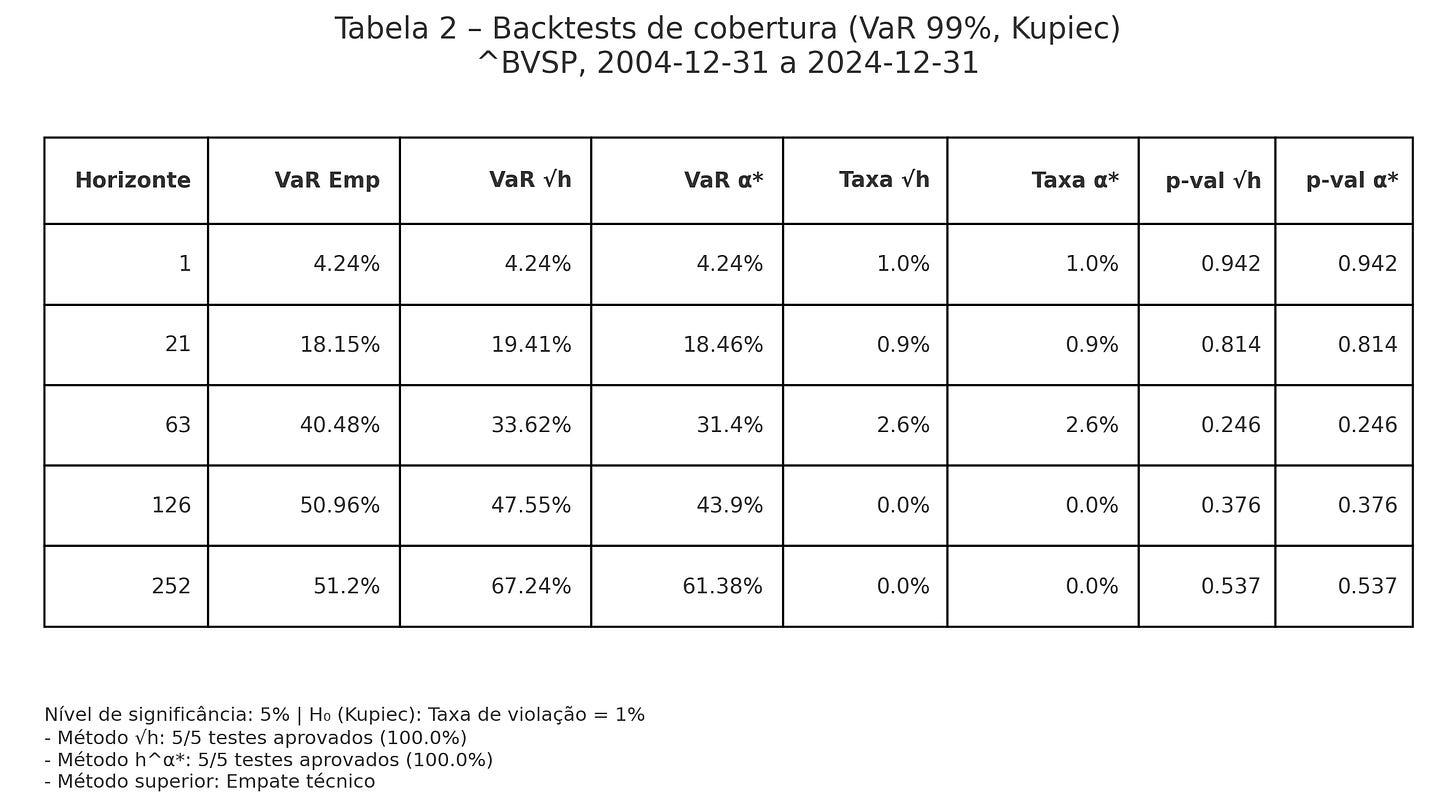
Cobertura por horizonte: onde raiz de h falha (e onde não falha)
Os backtests de Kupiec no VaR 99% mostram um quadro nuançado. Para 21 dias, as taxas de violação ficaram ~0,9% tanto para raiz quanto h elevado a α, com p-valores elevados: ambos adequados. Já em 63 dias, a taxa observada foi 2,6%, acima da meta de 1% (subcobertura), para os dois métodos; o p-valor (0,246) impede rejeitar a hipótese nula, mas sinaliza que a curva empíricaVaR 63d (40,48%) excede sensivelmente a regra da raiz (33,62%) e a regra de α (31,40%). Em 126 e 252 dias, não houve violações no período (amostra efetiva pequena em blocos não sobrepostos), o que torna os testes pouco informativos apesar de p-valores confortáveis.
Essas duas figuras deixam cristalino que:
a excelência do ajuste médio (R2 alto) não garante cobertura uniforme em todos os horizontes;
um único α pode subestimar a curva empírica no trimestre (63d), sugerindo curvatura — i.e., o escalonamento não é exatamente potência com expoente constante para todo h;
em janelas longas, o poder do teste despenca, de modo que aprovado não deve ser lido como conclusivo.
Então… α≈0,5: posso escalar à vontade?
Não. O achado α≈0,5 autoriza a regra da raiz como primeira aproximação, mas não como regra incondicional. Há três motivos principais:
Caudas pesadas (curtose ≈9,37) implicam convergência lenta do somatório de retornos para a normal — o quantil de cauda pode crescer mais rápido que raiz de h em janelas intermediárias, como o desvio observado em 63 dias sugere (MANDELBROT, 1963; MCNEIL; FREY; EMBRECHTS, 2015).
Mudança de regime faz α(t) oscilar no tempo; em subperíodos estressados, α pode superar e a raiz do tempo subestimar sistematicamente o VaR; em microestruturas dominantes, α pode cair abaixo de 0,50 (GATHERAL; JAISSON; ROSENBAUM, 2018).
Baixo poder amostral em janelas longas: pouquíssimos blocos não sobrepostos p-valores “confortáveis” não significam que o método seja realmente calibrado — apenas que o teste não tem potência para acusar erro (KUPIEC, 1995; CHRISTOFFERSEN, 1998).
Em síntese: não é recomendável escalar no escuro. É valido como hipótese inicial, mas com previsão de backtests por horizonte para ajustar quando necessário.
Alternativas
A ineficácia da regra da raiz do tempo para escalar o Value at Risk (VaR) exige a adoção de métodos mais robustos, com duas filosofias principais se destacando: a empírica e a condicional. A abordagem empírica descarta o escalonamento em favor da medição direta, calculando o VaR para cada horizonte de tempo a partir de blocos de dados históricos. Para prazos longos com pouca amostra, técnicas como o bootstrap ou a Teoria de Valores Extremos (EVT) oferecem estimativas mais confiáveis. Alternativamente, o paradigma condicional utiliza modelos como os da família GARCH, que são mais realistas e dinâmicos. Em vez de escalar um valor estático, um modelo GARCH projeta uma estrutura a termo da volatilidade que se adapta às condições atuais do mercado, capturando o agrupamento de volatilidade e a reversão à média.
Independentemente do modelo escolhido, a verdadeira robustez de um sistema de risco reside na disciplina de seu processo de validação. A adoção de métricas superiores como o Expected Shortfall (ES), que informa melhor sobre a severidade das perdas na cauda, é um passo importante. Contudo, o elemento mais crucial é a implementação de um framework de backtesting rigoroso que valide a performance do modelo em cada horizonte de tempo relevante para a decisão. A confiança não deve ser depositada no modelo em si, mas na força de seu processo de validação.
Encerramento
A análise do Ibovespa (2005–2024) revela um expoente α≈0,48 com alto R², uma descoberta que, à primeira vista, parece validar a regra da raiz de h. Essa aparente validação, porém, é enganosa. Ao inspecionar a curva por horizonte e aplicar backtests, notamos que a regra falha em janelas críticas, como a trimestral — um resultado esperado, dado que os dados exibem caudas pesadas e mudanças de regime. Assim, a prática mais segura é clara: a regra de bolso serve apenas como referência inicial. As decisões devem ser fundamentadas na curva de risco empírica, com validação por backtests formais e o suporte de métricas robustas. Afinal, o risco deve ser guiado pelos dados, não pelo hábito.
Referências
CHRISTOFFERSEN, P. F. Evaluating interval forecasts. International Economic Review, v. 39, n. 4, p. 841–862, 1998.
CONT, R. Empirical properties of asset returns: stylized facts and statistical issues. Quantitative Finance, v. 1, n. 3, p. 223–236, 2001.
FAMA, E. F. Efficient capital markets: A review of theory and empirical work. Journal of Finance, v. 25, n. 2, p. 383–417, 1970.
GATHERAL, J.; JAISSON, T.; ROSENBAUM, M. Volatility is rough. Quantitative Finance, v. 18, n. 6, p. 933–949, 2018.
KUPIEC, P. H. Techniques for verifying the accuracy of risk measurement models. Journal of Derivatives, v. 3, n. 2, p. 73–84, 1995.
MANDELBROT, B. B. The variation of certain speculative prices. Journal of Business, v. 36, n. 4, p. 394–419, 1963.
MCNEIL, A. J.; FREY, R.; EMBRECHTS, P. Quantitative Risk Management: Concepts, Techniques and Tools. 2. ed. Princeton: Princeton University Press, 2015.