Construindo a estrutura a termo da taxa de juros (ETTJ) de maneira independente

ETTJ Pré em Reais: uma abordagem independente e detalhada com Julia

Introdução

Neste artigo, mostrarei como construir, de forma detalhada, uma curva de juros pré-fixada usando informações do Tesouro Direto. O processo envolve:

• Coletar os dados dos títulos (preços unitários, datas de vencimento etc.)., já expliquei o passo a passo em Scraping de dados do Tesouro Direto.

• Identificar títulos prefixados zero-cupom (que não pagam cupom semestral), construindo uma curva inicial.

• Identificar títulos prefixados com cupom, cujo preço precisa de um método iterativo para se ajustar à curva.

• Por fim, integrar tudo em uma curva “completa” que seja consistente para todos os prazos.

O código está escrito em Julia. Cada função será detalhada, do que faz até seus argumentos e retornos. Ao final, gero um gráfico da curva em uma data de referência escolhida. O código completo está em interest_rate_points.jl e possui como pré-requisito o código de scraping que citei acima.

Este estudo tem diversas utilidades para quem deseja se aprofundar na construção de uma curva de juros e entender melhor a formação da Estrutura a Termo da Taxa de Juros (ETTJ). Primeiramente, ele se propõe a ser uma alternativa prática ao uso de provedores de referência, como a Anbima, permitindo que o pesquisador ou investidor monte sua própria curva de juros a partir dos dados disponibilizados pelo Tesouro Direto. Dessa forma, é possível conduzir análises independentes, sem ficar restrito a informações pré-processadas ou pagas.

Além disso, ao detalhar o passo a passo de como lidar com títulos que pagam cupom semestral, este material contribui para a compreensão mais ampla do processo de precificação, destacando os ajustes iterativos necessários para chegar a uma curva consistente. Também exemplificamos o uso da biblioteca InterestRates.jl, que pode ser usada de maneira mais geral, já que fornece ferramentas para interpolação, cálculo de taxas zero-cupom entre outros.

1. Dependências, tipos e constantes

• BRLBond agrupa:

  • type: tipo do título (por exemplo, “LTN”, “NTN-F”, “NTN-B Principal”, etc.).

  • maturity: data de vencimento em string, como "01/01/2029".

  • pu: preço unitário do título.

  • has_coupon: se tem cupom ou não (títulos zero-cupom retornam false).

• BR_CAL é o calendário de negócios adotado (Brasil).

• DAYS_IN_YEAR define 252 dias úteis por ano (convenção do mercado brasileiro).

• FACE_VALUE é o valor nominal de resgate do título, considerado R$1000.

• COUPON_ANNUAL_RATE é a taxa de cupom anual padrão que usaremos para os títulos que pagam juros semestrais (exemplo: 10% ao ano).

2. Funções auxiliares de conversão e datas

• has_coupon(bond_type::String): identifica se o tipo do título contém “Juros Semestrais” no nome, indicando que ele paga cupom.

• to_date(date_str::String): converte uma string no formato d/m/Y (dia/mês/ano) para um objeto Date do Julia.

• format_date(date::Date): faz a operação inversa, formatando um Date para o padrão brasileiro dd/mm/YYYY.

• yearfrac(start_date::String, end_date::String): calcula o fator de ano fracionário entre duas datas (dois strings), considerando apenas dias úteis (BusinessDays.bdayscount). Assim, o número final é dividido por DAYS_IN_YEAR (252).

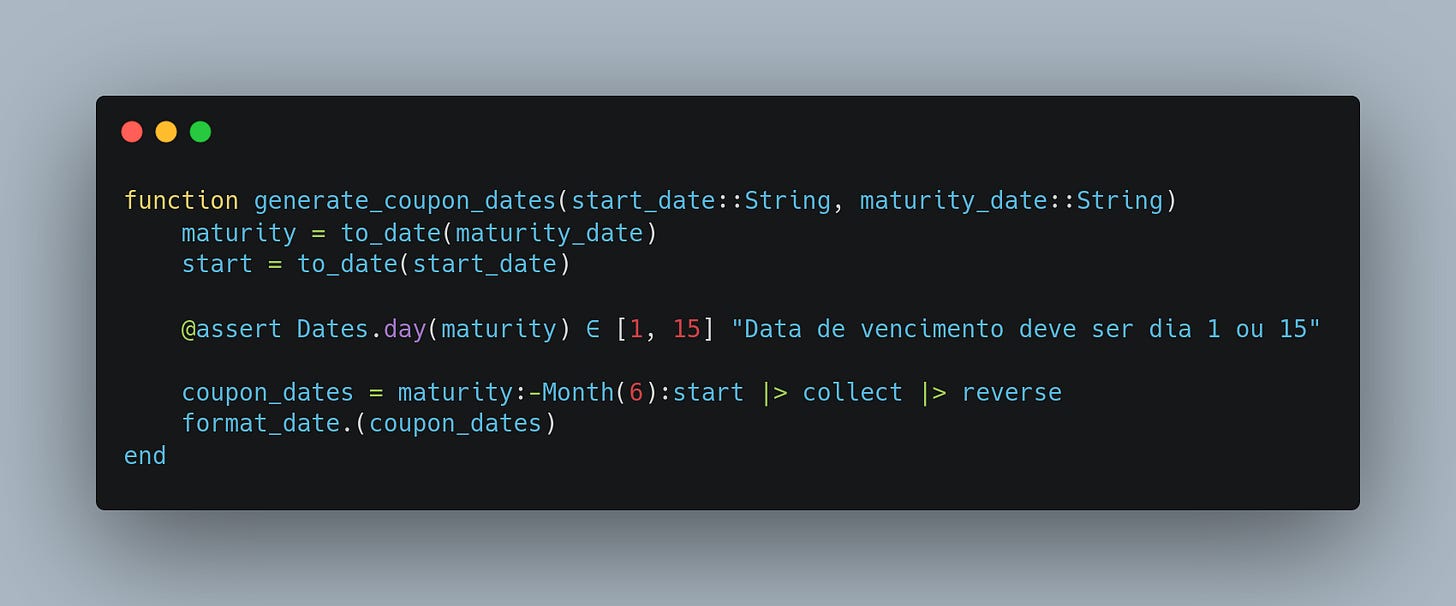
3. Geração de datas de cupom

Para títulos que pagam cupons semestrais, precisamos gerar as datas desses pagamentos entre a data de início (geralmente a data de compra ou a data de referência) e a data de vencimento.

• Usamos um range reverso maturity:-Month(6):start para obter as datas de pagamento de cupom de 6 em 6 meses, indo do vencimento para trás até o início.

• Depois, invertimos (reverse) essa lista para ficar em ordem cronológica e formatamos com format_date.

• A assert (@assert) garante que a data de vencimento seja dia 1 ou 15 (padrão Tesouro).

4. Cálculo de fluxo de caixa

Para precificar um título com cupom, precisamos saber quanto ele paga em cada data (fluxo de caixa). Títulos zero-cupom são mais simples: só pagam o valor de face no vencimento. Já os títulos com cupom pagam cupons semestrais e no último pagamento devolvem também o principal.

• face_value: valor de face (R$1000).

• annual_rate: taxa anual do cupom.

• is_bullet::Bool: se true, indica um título sem cupom (bullet), pagando tudo só no vencimento.

• semiannual_rate converte uma taxa anual (ex.: 10%) para a taxa equivalente semestral.

• coupon_dates obtém as datas semestrais.

• A expressão (coupon_value + face_value) ocorre somente no último pagamento (quando i == length(coupon_dates)).

5. Cálculo da taxa implícita (para zero-cupom)

Para encontrar a taxa de juros implícita em um título zero-cupom, resolvemos o problema:

\(\text{PU} = \sum_{(t_i, c_i) \in \text{fluxo}} \frac{c_i}{(1 + d)^{{\text{days}(t_i)}}} \)

onde days(t_i) conta quantos dias úteis existem até cada t_i​ e d é a taxa de juros diária implícita. Mas, como trabalhamos no anual, assumimos:

\((1 + \text{taxa_anual})^{\frac{1}{252}} - 1 = d\)

Usamos o pacote Optim para encontrar a taxa que faz o preço presente igual ao PU de mercado.

• pu: preço unitário do título (média de compra e venda, por exemplo).

• pu_date: data na qual o PU é válido (data de referência).

• cash_flow: vetor de tuplas (data_do_pagamento, valor_pago_nessa_data).

• objective(rate): define a função que calculamos para cada taxa candidata. A diferença (em valor absoluto) entre o fluxo descontado e o PU é o que queremos minimizar.

• optimize(...) usa o método Brent para buscar entre 0 e 100% de taxa (0,0 a 1,0) a que melhor se encaixa.

6. Construindo a curva zero-cupom

A curva zero-cupom é construída somente com títulos que não têm cupom. Para cada título zero-cupom, calculamos a taxa implícita e armazenamos num Dict{Date, Float64}, que mapeia data de vencimento → taxa anual.

• zero_coupon_bonds são só os títulos sem cupom.

• Para cada bond, chamamos calculate_implied_rate passando um fluxo de caixa que paga R$1000 apenas no vencimento ((bond.maturity, FACE_VALUE)).

• Preenchemos o dicionário com a data de vencimento como chave e a taxa calculada como valor.

7. Ajuste iterativo (títulos com cupom)

Para os títulos que pagam cupom semestral, precisamos de um passo adicional. A taxa de cada título depende da curva – e a curva, por sua vez, depende das taxas de todos os títulos. Então, faz-se um ajuste iterativo:

1. Começamos com a curva zero-cupom como ponto de partida.

2. Para cada título com cupom, ajustamos a taxa de vencimento desse título para que o preço calculado (usando price_with_coupon) case com o observado.

3. Atualizamos a curva com essa nova taxa e passamos para o próximo título.

• adjusted_curve começa como cópia da curva zero-cupom.

• Para cada título com cupom (isto é, que tenha has_coupon == true):

  • Gera-se o fluxo de caixa com calculate_cash_flow.

  • Define-se uma função objective(rate) que:

    • Insere rate na curva no vencimento específico daquele título.

    • Usa a função price_with_coupon para precificar esse título com a curva momentaneamente ajustada.

    • Calcula o desvio em relação ao preço de mercado (observed_price).

  • Chama-se optimize(objective, 0.0, 1.0, Brent()) para encontrar a taxa que minimiza a diferença.

  • Substitui-se na curva a nova taxa encontrada para aquele vencimento.

No final, adjusted_curve é retornada com as taxas de vencimento ajustadas para todos os títulos com cupom.

8. Construindo a curva completa (integra zero-cupom + cupom)

Nesta função, juntamos tudo. Dividimos a lista original de títulos entre zero-cupom e com cupom. Construímos a curva zero-cupom e depois chamamos o passo de ajuste iterativo para obter a curva final.

build_complete_yield_curve:

1. Separa os títulos em zero_coupon_bonds e coupon_bonds.

2. Constrói a zero_coupon_curve.

3. Ajusta iterativamente para cupom em complete_curve.

4. Cria um objeto IRCurve do pacote InterestRates, fornecendo datas (em dias úteis), taxas e a convenção de capitalização (exponential compounding).

5. Gera um dicionário diário (daily_curve) para cada dia útil entre a primeira e a última data de vencimento, obtendo a taxa zero correspondente através de InterestRates.zero_rate(curve, current_date).

9. Interpolação e precificação de título com cupom

• create_curve recebe o Dict com datas de vencimento → taxas e as converte em uma curva de juros (IRCurve).

• price_with_coupon usa a curva criada para obter o fator de desconto (discountfactor) de cada data de pagamento e acumula o valor presente total.

10. Plotando a curva completa

Por fim, vamos criar um gráfico para visualizar a curva. A função plot_complete_curve recebe nosso dicionário de data → taxa, converte tudo para anos (dividindo o número de dias úteis por 252) e plota a curva de yield contra o prazo.

• Calculamos days como a diferença em dias úteis entre a data de referência e cada vencimento, depois dividimos por DAYS_IN_YEAR para transformar em frações de ano.

• A linha plot(...) gera o gráfico.

• Adicionamos marcações (annotate!) em cada intervalo de 0.5 ano, mostrando a taxa (em %) aproximada.

• Se output_file não for nothing, salvamos a figura.

11. Executando tudo

Finalmente, escolhemos uma data de referência, carregamos dados reais do Tesouro (via função load_treasury_data(), que vem do arquivo scraping_tesouro.jl), filtramos para pegar apenas títulos pré-fixados e construímos a curva:

• load_treasury_data() e filter_treasury_bonds(...) são funções do seu arquivo de scraping que retornam a tabela de preços do Tesouro em formato DataFrame.

• type="PRE" filtra apenas os títulos pré-fixados.

• Transformamos cada linha (eachrow(filtered_df)) em um BRLBond. Para o PU, fazemos a média entre o “PU Compra Manha” e “PU Venda Manha”, convertendo vírgulas em pontos para Float64.

• Por fim, construímos a curva com build_complete_yield_curve e a plotamos com plot_complete_curve, salvando em “yield_curve.png”.

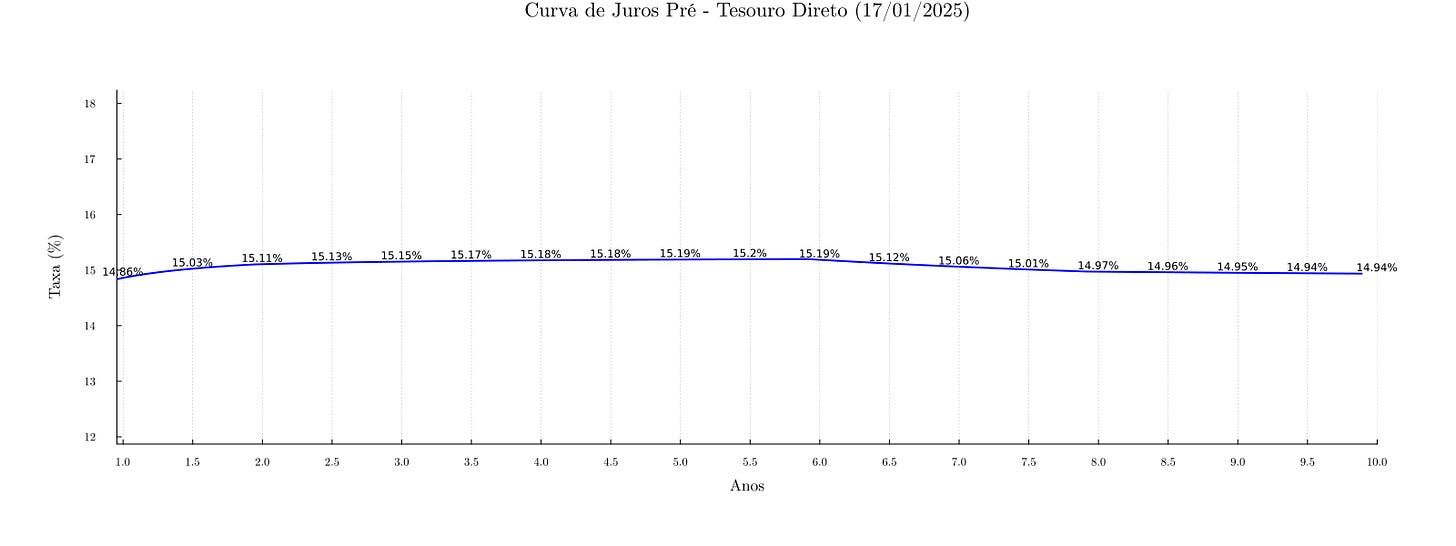
Abaixo, o resultado da curva para um dia específico (17/01/2025):

Vale também destacar as seguintes ressalvas:

• Base de dados: Os preços e yields utilizados são os informados pelo Tesouro Direto na abertura (manhã), não refletindo o mercado secundário como no caso do utilizado pela Anbima.

• Vértices de curto prazo: Podemos ter lacunas (falta de títulos com vencimentos próximos) e, consequentemente, pouca informação para a parte curta da curva.

• Extrapolação: Não fazemos extrapolação para além das datas coletadas por segurança, evitando assumir comportamentos para os quais não há dados suficientes.

Até a próxima!