Preferências e otimização de carteiras: da utilidade à escolha ótima
Da teoria à prática na construção de portfólios alinhados ao perfil de risco
Em finanças, uma das questões mais importantes para qualquer investidor é: como encontrar a carteira que melhor reflita minha aversão ao risco? Essa pergunta, por sua vez, se conecta a uma série de conceitos fundamentais e pode ser orientada a algumas ideias das teorias de carteiras: curvas de indiferença, função de utilidade média-variância (e sua ligação com a CRRA, ou Constant Relative Risk Aversion), e o certainty equivalent. Neste artigo, vamos explorar cada um desses pontos, de forma integrada, para esclarecer como eles ajudam a traduzir preferências de risco em escolhas de investimento.
1. Curvas de indiferença: mapeamento de preferências
O que são curvas de indiferença?
As curvas de indiferença surgem na teoria microeconômica para representar todas as combinações de risco e retorno (ou outras variáveis) que proporcionam o mesmo nível de utilidade a um investidor. No plano de dois eixos — em finanças, costumamos usar retorno esperado no eixo vertical e desvio padrão (volatilidade) no eixo horizontal — cada curva de indiferença marca um “contorno” de utilidade fixa.
Intuição: se um ponto AAA (carteira) e um ponto BBB (outra carteira) estão na mesma curva, significa que o investidor não tem preferência por AAA nem por BBB; ambos geram o mesmo bem-estar. Se formos capazes de desenhar muitas dessas curvas, cada uma representando níveis de satisfação diferentes, fica claro que as curvas mais “no alto e à esquerda” (maior retorno esperado e menor risco) são mais desejáveis.
Relação com aversão ao risco
Quanto mais avesso ao risco for o investidor, mais inclinadas (ou “verticais”) tendem a ser as curvas de indiferença. Isso reflete o fato de que ele exige uma compensação maior em retorno sempre que o risco (volatilidade) aumenta. Por outro lado, um investidor mais tolerante ao risco tem curvas mais “planas”, pois aceita aumentos de risco com menos incremento de retorno.
2. Função de utilidade média-variância (mean-variance)
O conceito
A abordagem de Média-Variância (ou mean-variance) foi popularizada por Harry Markowitz. A ideia central é que o investidor se preocupa com dois parâmetros:
Retorno Esperado (média)
Risco (medido pela variância ou desvio padrão)
Na forma mais simples, a função de utilidade média-variância pode ser escrita como:
onde:
E(rp) é o retorno esperado da carteira ppp;
Var(rp) é a variância desse retorno;
γ é o coeficiente de aversão ao risco do investidor.
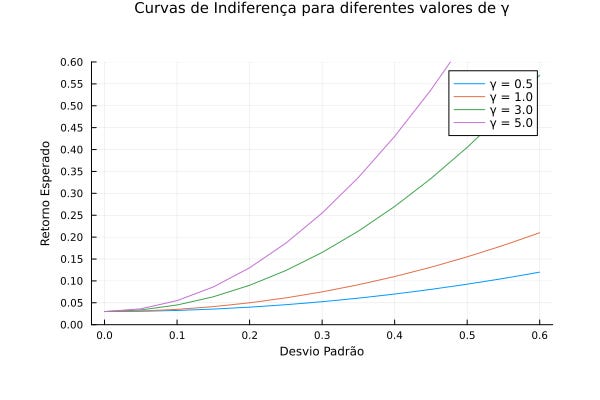
Nessa fórmula, o investidor “gosta” de E(rp) (retorno) e “desgosta” de Var(rp), e a intensidade dessa aversão é controlada por γ. Abaixo, variás curvas de indiferença com coeficientes de aversão ao risco diferentes.
Ligação com a CRRA (constant relative risk aversion)
A CRRA é outra forma de expressar a utilidade de um investidor, muito utilizada em modelos de horizonte de longo prazo e em finanças quantitativas. A função de utilidade CRRA assume a forma:
onde W é a riqueza (ou consumo) e γ (o mesmo símbolo, mas agora num contexto levemente diferente) é o coeficiente de aversão ao risco relativa.
Em muitos casos, quando as distribuições de retornos são próximas de normais (ou para pequenos intervalos de tempo), mean-variance e CRRA acabam produzindo decisões de alocação muito parecidas.
Na prática, a CRRA enfatiza que a utilidade marginal decresce com a riqueza, mantendo proporcionalidade (ou seja, você se torna menos sensível a variações absolutas de dinheiro quando já tem muito capital, mas a aversão relativa ao risco permanece constante).
3. O conceito de certainty equivalent
Definição
O certainty equivalent (ou equivalente de certeza) de um investimento é o valor certo que o investidor aceitaria em vez de participar de um jogo/retorno incerto com mesma utilidade. Em termos simples, ele responde à pergunta:
“Quanto de retorno garantido você precisaria receber para ficar indiferente entre aceitar esse valor certo e entrar num investimento arriscado específico?”
Matematicamente, se a utilidade esperada do investimento arriscado é
então o certainty equivalent CE satisfaz:
Papel na escolha de carteiras
O certainty equivalent é muito útil para comparar estratégias de investimento em termos de valor em dinheiro, pois expressa quanto vale, em reais (ou dólares etc.), a utilidade de uma estratégia que tem risco. Assim, se você tem duas carteiras com utilidades diferentes, basta transformar cada utilidade em seu certainty equivalent e verificar qual tem valor monetário maior.
4. Como encontrar a carteira que representa a aversão ao risco do investidor?
4.1. O problema de alocação
Definir o perfil de risco: o investidor deve ter clareza sobre sua γ (aversão ao risco). Isso pode ser estimado por questionários, discussões com assessores financeiros ou mesmo pela revelação de preferências (como a proporção de renda que a pessoa se dispõe a colocar em ativos de maior risco).
Estimar retornos e riscos: para cada classe de ativos (ações, títulos de renda fixa, fundos imobiliários, etc.), é preciso ter estimativas de retorno esperado, volatilidade e correlações (pois a correlação determina o grau de diversificação).
Resolver o otimizador de carteira: normalmente, formula-se o problema:
\(\max_{\,w} \quad E(r_p) \;-\; \frac{\gamma}{2}\,\mathrm{Var}(r_p),\)sujeito a
\(\sum_i w_i = 1\)e se houver restrições (por exemplo, não vender a descoberto), adicionar wi≥0 ou equivalentes.
4.2. Interpretação via curvas de indiferença
Cada investidor, com γ diferente, terá curvas de indiferença diferentes.
Graficamente, a carteira ótima aparece como o ponto de tangência entre a curva de indiferença de maior utilidade e a fronteira de mínima variância (ou fronteira eficiente).
4.3. Determinação do certainty equivalent
Uma vez encontrada a carteira ótima (para aquela γ), podemos converter a utilidade resultante em certainty equivalent. Esse valor é a “renda fixa” imaginária que teria o mesmo efeito em termos de satisfação. É um número que ajuda o investidor a compreender, em termos de valor certo, a atratividade de uma carteira que é, na realidade, arriscada.
Na figura abaixo, caso o coeficiente de aversão ao risco seja 5, na carteira da fronteira eficiente que tangencia a curva de indiferença (73,6% de bonds e 26,4% de stocks), o certaint equivalent é o cruzamento com o eixo y (0,0309) da curva de indiferença que tangencia a fronteira eficiente.
Os conceitos de curvas de indiferença, utilidade média-variância e CRRA, juntamente com o certainty equivalent, formam a espinha dorsal de muitos modelos de alocação de carteira. Eles nos lembram que:
Investir é sobre trade-offs entre retorno e risco.
Cada investidor tem um grau de aversão ao risco que influencia a escolha ótima.
O certainty equivalent traduz a satisfação (utilidade) de uma carteira arriscada em termos de “quanto em valor certo” a pessoa aceitaria para abrir mão daquela oportunidade.
A diversificação é fundamental para reduzir riscos sem necessariamente abrir mão de retornos mais altos, pois ativos com correlação baixa podem compensar mutuamente suas oscilações.
Porém, como explicado nos artigos Teoria moderna de portfolio de Markowitz: uma relíquia educacional? e Sharpe Ratio: por que continua sendo um dos indicadores de risco-retorno mais usados, há diversas simplificações adotadas nessa abordagem e a principal e que impacta o resultado que obtemos é a suposição de que a variância é, de fato, uma boa medida para o risco, algo que não é observado na prática.
O código Julia que gerou as imagens deste artigo estão disponíveis em pq_mv_indif.
Até a próxima!